
Module 2 Unit 6 - Algorithmic Notation#
Unit Learning Objectives#
By the end of this unit, you will be able to
Identify For loops, While loops, if/then statements
Use them for repetitive tasks
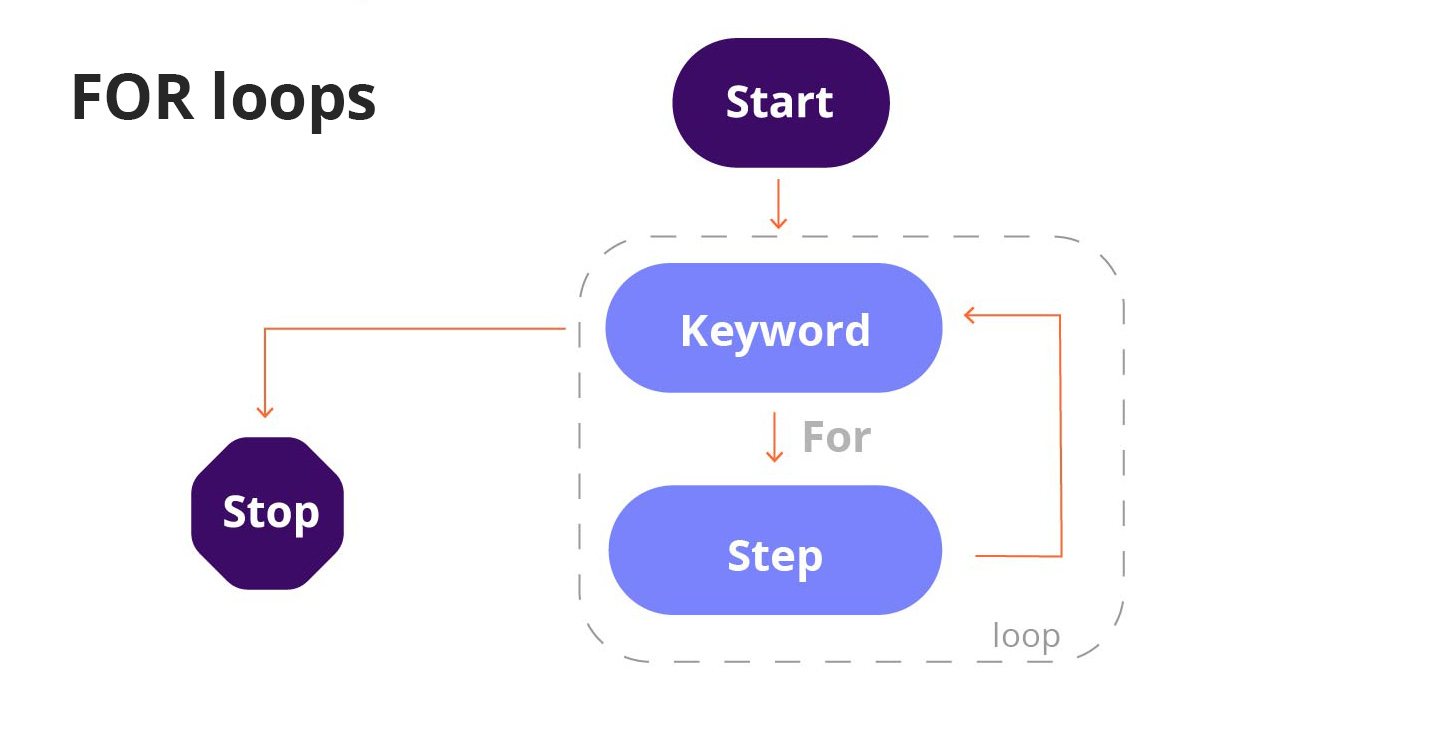
FOR Loops#
Algorithmic notation is the use of keywords that represent a specific type of step on a solution. These keywords allow the representation of more efficient solutions.

For example, every time you have to repeat a step, it is easier to use a special keyword, in comparison repeating that step over an over in the solution.
Let’s start with the example of going to your classroom in the morning. If you had to explain how to go from the parking lot to your classroom to someone else, you can use very explicit instructions such as: Get out of your car
Move 1 meter
Move 1 meter
Move 1 meter
Move 1 meter
Move 1 meter
Turn left
Move 1 meter
Move 1 meter
Move 1 meter
Turn right
Move 1 meter
Move 1 meter
Move 1 meter
Turn left
Open the door
Move 1 meter
You have arrived
Can you think of a way to simplify this set of instructions? One way is to use the keyword FOR to indicate a specific number of times that an action needs to be repeated. In the example above, we can simplify the steps to get to your classroom as follows:
Get out of your car
FOR 5 times repeat: Move 1 meter
Turn left
FOR 3 times repeat: Move 1 meter
Turn right
FOR 3 times repeat: Move 1 meter
Turn left
Open the door
FOR 1 time repeat: Move 1 meter
You have arrived
Knitting Example#

Let’s use the example of a knitting “algorithm” to make a scarf to show the use of the keyword FOR to indicate that a step should be repeated for a specific number of times. Using our own words, we can write the knitting scarf algorithm as follows:
Gather your two knitting needles and a large ball of wool.
Make a stitch at the start of a row
2a. Make another stitch.
2b. Make another stitch.
2c. Make another stitch.
2d. Make another stitch.
2e. Make another stitch. … 2zz. Make a final stitch.
On a new row, “knit one, pearl two”
2a. “knit one, pearl two”
2b. “knit one, pearl two”
2c. “knit one, pearl two”
2d. “knit one, pearl two”
2e. “knit one, pearl two” … 2zz. “knit one, pearl two”
On a new row, “knit one, pearl two”
2a. “knit one, pearl two”
2b. “knit one, pearl two”
2c. “knit one, pearl two”
2d. “knit one, pearl two”
2e. “knit one, pearl two” … 2zz. “knit one, pearl two” …
This gets tedious really fast. We can summarize this algorithm in our own words as follows:
Gather your two knitting needles and a large ball of wool.
Cast on a row of 39 stitches to start the scarf.
On a new row, repeat the pattern “knit one, pearl two” 39 times.
Repeat step 3 for each row in the scarf, 125 times.
Bind of in a stitch pattern, to knot the end of the scarf into final form.
Sew in ends, wash gently by hand, block and let air dry.
This is a more detailed list of instructions and can be considered an algorithm for making a scarf. Notice that some instructions basically say to do one thing (e.g grab your needles), while other instructions ask you to repeat some action (e.g. make 39 stitches. Or knit one, pearl two repeatedly to the end of the row). These repeated actions are examples of loops, which come up often in computer algorithms.
Now using the keyword FOR to represent a loop in the knitting scarf algorithm we would have the following simplified notation:
Gather your two knitting needles and a large ball of wool.
FOR 39 times repeat: cast a stitch on your needle to start the scarf.
FOR 39 times repeat: “knit one, pearl two”
Repeat step 3 for each row in the scarf, 125 times.
Bind of in a stitch pattern, to knot the end of the scarf into final form.
Sew in ends, wash gently by hand, block and let air dry.
Notice that step 5 in the algorithm above is still using the word Repeat instead of FOR. This is because FOR. to use FOR in this algorithm, we have to use a special notation called a “nested loop”. On a “nested loop” we put a loop inside another loop as follows:
Gather your two knitting needles and a large ball of wool.
FOR 39 times: cast a stitch on your needle to start the scarf.
FOR 125 times repeat:
3a. FOR 39 times repeat: “knit one, pearl two”Bind of in a stitch pattern, to knot the end of the scarf into final form.
Sew in ends, wash gently by hand, block and let air dry.
LOOPS and NESTED LOOPS#
Loops come up whenever an algorithm has to repeat some action over and over again. Additional examples of LOOPS include:
When sorting books on a shelf in alphabetical order, you need to repeat the same action for each book over and over.
When baking a recipe, you need to add multiple cups of a specific ingredient. E.g. sugar.
The same thing happens with computer code. For instance, suppose you want to print 10 numbers, and their square. In human form, and computer form, you might write the following:
Human Language |
Computer Code |
|---|---|
On line one, print the answer to 1 times 1 |
print(1,1*1) |
On line two, print the answer to 2 times 2 |
print(2,2*2) |
On line three, print the answer to 3 times 3 |
print(3,3*3) |
On line four, print the answer to 4 times 4 |
print(4,4*4) |
On line five, print the answer to 5 times 5 |
print(5,5*5) |
On line six, print the answer to 6 times 6 |
print(6,6*6) |
On line seven, print the answer to 7 times 7 |
print(7,7*7) |
On line eight, print the answer to 8 times 8 |
print(8,8*8) |
On line nine, print the answer to 9 times 9 |
print(9,9*9) |
On line ten, print the answer to 10 times 10 |
print(10,10*10) |
Again, this gets dull really fast. A better way is to write a loop. A “for” loop will work, like this:
FOR n in range(1,10):
print(n,n*n)
Examining this code carefully, it says that the number n will be set to the values 1,2,3,…,10, and print out the value of n and n*n, in succession.
Conditional Statements#
What if you are writing an algorithm but you need to represent two or more different options? In this case, the keyword IF becomes quite useful. IF is used when you want to write a statement or step to evaluate if a condition has been met. That’s why IF is also called a “conditional statement”.

Examples of cases when a “conditional statement” is useful include:
In baking: IF the butter is cold, warm it up before adding it to the dish
When following directions: IF you are facing south, turn around until you face north.
Next, how do you indicate what happens when the condition is not met? In this case, we follow IF with an ELSE statement.
Examples of cases to use ELSE:
In baking:
IF the butter is cold:
warm it up and then add it to the dish
ELSE
Add it to the dish
When following directions:
IF you are facing south:
tourn around until you face north and start walking in that direction
ELSE
Start walking
Knitting scarf algorithm An IF/ELSE conditional statement can be useful when making a scarf for a child vs. an adult. For example:
Gather your two knitting needles and a large ball of wool.
FOR 39 times: cast a stitch on your needle to start the scarf.
IF (scarf is for a child) THEN:
FOR 125 times repeat:
FOR 39 times repeat: “knit one, pearl two”
ELSE
FOR 225 times repeat:
FOR 39 times repeat: “knit one, pearl two”
Bind of in a stitch pattern, to knot the end of the scarf into final form.
Sew in ends, wash gently by hand, block and let air dry.
With computer code, we can use the print number example with a variation such as that when we get to the number 5, we multiply it times 10, instead of doing a square, as follows:
FOR n in range(1,10):
IF (n = 5) THEN
print(n,n*10)
ELSE
print(n,n*n)
While Loops#
A WHILE loop is similar to a FOR loop with the main difference that a WHILE loop includes a “conditional statement”. A FOR loop is used to indicate a number of times to repeat an action. A WHILE loop is used to indicate every specific number of times an instruction needs to be repeated. A WHILE loop is used to repeat a list of instructions until some condition is met .
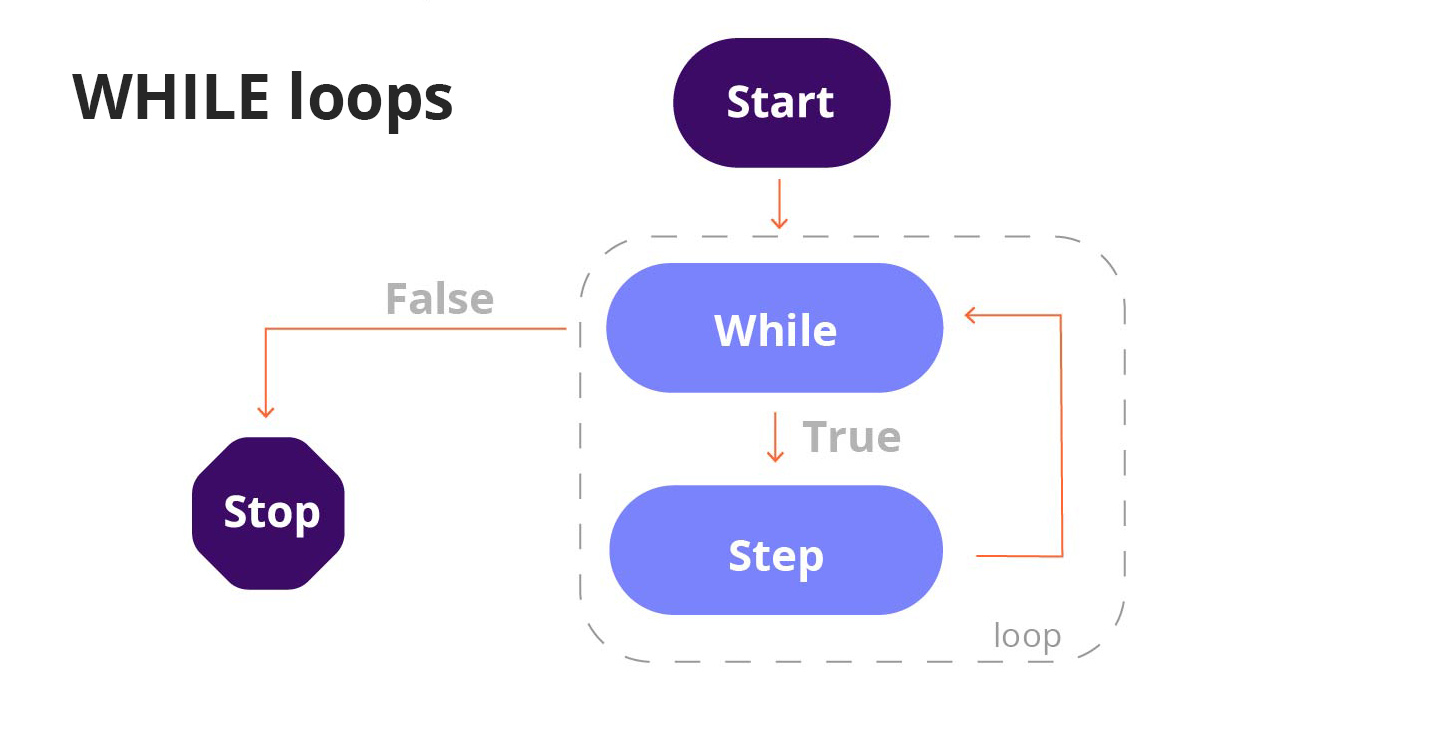
Examples of cases when a WHILE loop is useful, include
In baking: WHILE mixture is lumpy, keep mixing
When following directions: WHILE you haven’t reached the door, keep walking
In the knitting scarf example, for instance, if we are not sure about the specific number of rows in a scarf we can change the algorithm as follows:
Start a row with Knit 1, Pearl 2.
While you’re not at the end of the row yet
Do another Knit 1, Pearl 2.
With computer code we can use the WHILE loop to repeat a task until a condition is met, for example, printing numbers until we reach 100: WHILE (n < 100)
print(n,n*n)
Activity#
Can you write out a loop that prints out the first 10 even numbers? (2,4,6, etc).
In the knitting example, there is one loop that make 39 stitches on each row, another loop that adds row after row. Suppose you have 100 rows – how many stitches will there be altogether?
(hint: it is a lot more than 130.) These are called “nested loops” and can summarize a large number of operations as two simple loops.
When you mark papers, do you mark question 1 for all students, before marking question 2, and so on? Or do you mark questions 1,2,3,4… for the first student, then all questions 1,2,3,4… for the second student, and so on? You might note that some teachers do it one way, some the other. Are these loops? Nested loops?
Can you write two different algorithms, using “for” loops, to do the two different ways of marking student assignments as described above?
In the next module, we will take these ideas and apply them to a concrete task.
Glossary#
Algorithm A list of step-by-step instructions to complete some well-defined task.
Compiler/Interpreter a piece of software that reads instructions for the computer, and translates it into actions by the hardware. These actions could be to move data from one place to another, to do arithmetic calculations with actual data, display an image on a screen, and so on.
Computer Hardware The physical part of the computer, that includes some memory to store information and instructions, a processor that can do the things listed in the instructions, input and output devices (keyboards and screens, for instance) to move information in and out, and often a calculating unit that can do arithmetic on numbers that are stored as data.
Loop A part of an algorithm that gets repeated over and over.
Software Instructions and algorithms for a computer, written in a “language” that can be read and understood by a computer.

