Binary decimal conversion¶

Introduction¶

A positional numeral system is a way of writing numbers using place value.
Our usual way of writing numbers is an example:
In a number like 1234, the 4 is in the ‘ones’ spot, the 3 in the ‘tens’ spot, and so on.
Each position represents a power of 10, so we call this the decimal, or base-10 system.

This notebook will look at positional numeral systems in general, but a focus on two familiar examples:
The decimal (base-10) system we all know and love, and the binary (base-2) system.

Topics include:

the base of the numeral system
how the choice of base effects the digits we use to write a number
how to convert between decimal and binary representations of a number.

Big Ideas¶

Here are some key takeaways you should have in mind as you progress through this notebook:

Computers understand numbers in binary, while humans understand decimal.
Conversion from decimal to binary is fundamental to human-computer interaction.
Understanding this process requires only basic arithmetic: addition, subtraction, and powers.

Background information¶

Numeral systems¶

In mathematical terminology, a number system refers to the type of number being used.
Number systems include the integers, the rational numbers (fractions), and real numbers.
A numeral system refers to the way we write those numbers down.

The numeral system we use when we write a number like 3127 is called the decimal system.
You’ve gotten so used to using the decimal system that you understand the number 3127 without thinking!
Take a moment to remind yourself that the position of each digit represents a value: 1, 10, 100, etc.
The digit in that position then tells us how many of that quantity we have.
In 3127, there are 3 thousands, one hundred, two tens, and seven ones.

But our method of expressing numbers is by no means universal.
Another numeral system you’ve probably encountered is that of Roman numerals.
The Roman system uses symbols instead of position to represent certain quantities.
We count how many times each symbol appears to know how many of that quantity we have.

For example, the Roman numeral system uses I for 1, V for 5, X for 10, C for 100, and D for 1000, among others.
In the Roman system, the number 3127 is written as MMMCXXVII:

\[\begin{split}\begin{aligned} 3127&=3000+100+20+7\\ & = \underbrace{1000+1000+1000}_{\text{M M M}}+\underbrace{100}_{\text{C}}+\underbrace{10+10}_{\text{X X}}+\underbrace{5}_{\text{V}}+\underbrace{1+1}_{\text{I I}}. \end{aligned}\end{split}\]

Note that in the Roman system, there is no symbol for zero: a number like 210 has no ones, so we don’t write any.
The number 210 is written CCX. Many early numeral systems did not have a zero.
The invention (discovery?) of zero is usually credited to India, around the 4th or 5th century.
However, zero was also used in Mayan calendars.
The number zero is an interesting topic in its own right, but it’s not the subject of this notebook.
If you’re curious, you might enjoy this Scientific American article.

Binary and decimal numbers are two examples of positional numeral systems, where the relative placement of digits tells us about the values they represent.
One of the earliest examples of a positional system is the remarkable Babylonian sexagesimal (base-60) system.

Our numeral system traces its origins back to India and the Middle East, and is known as the Hindu-Arabic numeral system.
This is a decimal system, where positions represent powers of 10, and symbols represent numbers from 0 to 9.
For example, as we mentioned above, the expression 3127 is convenient shorthand for

\[3\times 1000 + 1\times 1000 + 2\times 10 + 7\times 1.\]

Notice that 1000, 100, 10, and 1 are all powers of 10: $1=10^0, 10=10^1, 100=10^2$, and $1000=10^3$.
When each position represents successive powers of some number, we call that number the base of the system.
The decimal system uses base 10. The binary system, which is essential to computing, uses base 2.

Why Binary?¶

Why do computers use binary? First, we might ask: why do we use decimal?
We’ve been using decimal so long, you may not have wondered why we chose the base-10 number system for our everyday number needs.
(There’s a pretty good chance that it has something to do with humans having 10 fingers.)

Regardless of what led to it, tricks we’ve learned along the way have solidified base-10’s place in our heart.
Everyone can count by 10s. We even round large numbers to the nearest multiple of 10. We’re obsessed with 10!

Computers, being electronic machines, only understand two things:
‘ON’ or ‘1’: electricity is flowing (through circuit, gate, transistor, whatever).
‘OFF’ or ‘0’: electricity is not flowing.

In a computer, everything must be represented as collections of ONs and OFFs. Unfortunately, this scheme is difficult for humans to process.
To make things easier on ourselves, humans represent “computerian” as binary numbers:

ON is represented by a 1, and OFF is represented by a 0.
So instead of “OFF ON ON OFF”, we humans can read or write this as “0110”. |

Base and Digits in a Positional System¶

The base in a positional numeral system like Hindu-Arabic is the number whose powers we represent by the position of the digits in a number.
Note that the value of the base is also the number of different symbols we need for digits.
For example, the decimal (base-10) system uses 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
In some computer applications (like many WiFi passwords) a hexadecimal (base-16) system is used, with digits

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f.

Of course, we also use “base” to refer to the number that gets multiplied when applying an exponent.

Examples:

In $8^{2}$, 8 is the base, and the result is $8 × 8 = 64$.
In $5^{3}$, 5 is the base, and the result is $5 × 5 × 5 = 125$.

This isn’t really a coincidence, since we use powers of the base to reconstruct numbers from positional notation.
The way our notation works is as follows:

Position of a digit (read from right to left) tells us which power of the base to use.
The digit in that position tells us what to multiply that power by.

Any integer greater than 1 can be used as a base. (Why can’t we use 1?)
For a hypothetical “base-$r$” system, we would have $r$ symbols to represent the digits, and each position represents a power of $r$.
For example, we could imagine a base-26 system with each letter of the alphabet representing a digit.
(It’s doubtful anyone would want to use this system, but we can imagine it!)
In this system, the word “number” would actually be a number!
If we assign each letter its place value in the alphabet, we have $$ n = 14, u = 21, m = 13, b = 2, e = 5, r = 18, $$

and

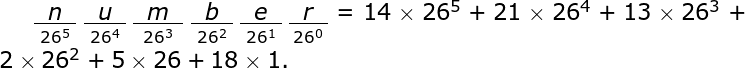
This doesn’t seem very practical, however, so let’s sum up the key points and move on to numbers in decimal and binary.

The base of a positional numeral system is equal to the number of digits (symbols) needed to represent numbers in that system.
The position of a digit tells us what the corresponding power of the base should be.
We multiply that power by the value of the digit, for each digit present.
Finally, we add everything up to get our number.

For a number $a_na_{n-1}\cdots a_2a_1a_0$ with digits $a_0, a_1, \ldots, a_n$ written in base $r$, we get the number

\[a_nr^n+a_{n-1}r^{n-1}+\cdots a_2r^2+a_1r+a_0.\]

We won’t do it here, but see if you can convince yourself any number can be written uniquely in any base. We never miss a number, and we never have two different ways of writing down the same number.

While working with numbers of different bases, its best to put the base as a subscript to the number to avoid confusion like $(Number)_{Base}$. For example in order to represent a binary number we place 2 as a subscript like $(11)_{2}$ and 10 to denote decimal numbers like $(11)_{10}$.

An answer to an impractical problem.¶

In the example above, were you left wondering what (base-10) number is “number” in (base-26)?
We can ask the computer to calculate it for us:

14*26**5 + 21*26**4 + 13*26**3 + 2*26**2 + 5*26 + 18

176165748

Counting in binary¶

We can count in decimal endlessly, even in our sleep, but how can we count in binary?
Zero and one in base-two should look pretty familiar: 0 and 1. From there things get decidedly binary.

In decimal, we start in the ‘ones’ position, and count until we run out of digits: $$0, 1, 2, 3, 4, 5, 6, 7, 8, 9.$$ After 9, we hit the next power of 10, so we add 1 to the 'tens' position, and reset the'ones' to 0.<br> Then we go back to counting in the 'ones' position until we reach 9 again: $$10, 11, 12, 13, 14, 15, 16, 17, 18, 19.$$ Now, we increase the ‘tens’ digit by 1 again, and reset the ‘ones’, getting 20.
We continue like this until we reach 99, and then we’re ready to add a 1 in the ‘hundreds’ position.
When we do, the digits in both the ‘tens’ and ‘ones’ positions reset to zero, and then we continue the process.

Counting in binary is similar, with two important differences:

Positions represent powers of 2, not 10: $ 2^0=1, 2^1 = 2, 2^2 = 4, 2^3 = 8, 2^4 = 16, 2^5 = 32, 2^6=64$, etc.
Digits are only 0 and 1, so the ‘change position and reset to zero’ step is a lot more frequent!

Remember that we’ve only got those two digits, so as we do in decimal, when we run out of symbols we shift one column to the left, add a 1, and turn all of the digits to the right of that column to 0.
So after 1 we get 10, then 11, then 100. Let’s start counting…

Decimal	Binary
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

Converting between decimal and binary notation.¶

Converting binary to decimal¶

Mathematically, this is straightforward. The digits in binary are called bits.
Each position represents a power of 2. We multiply each power of 2 by the bit in that position, and then add it all up.

Example:¶

To convert the number 1101 from binary to decimal, we compute as follows: $\begin{aligned} 1101 &= 1 * 2^{3} + 1 * 2^{2} + 0 * 2^{1} + 1 * 2^{0} \\ &= 1*8+1*4+0*2+1*1\\ &= 8+4+1\\&=13 \end{aligned}$

Interactive Method¶

We will now demonstrate an interactive approach to doing this conversion.
Our implementation uses buttons on a computer screen, but you can do this “in real life” as well!

For demonstration we start off with a 5 bit number; that is, a 5 digit binary number, which can represent up to 31 in decimal.

Represent each binary digit with a single card, so there will be 5 cards.
Mark one side of each card with a power of 2: our five cards will be 1, 2, 4, 8, and 16.
Mark the other side with a 0.
Arrange the cards to reflect our positional system: Our order is 16, 8, 4, 2, 1.
The side with the power of 2 represents 1 in binary and the other side represents 0.
Start with the 0 on each card. Choose a binary number, then flip the cards whose digit is 1.
For example, if we chose the number 11001, we flip the 16, the 8, and the 1.
Now to convert to decimal we just add up the numbers showing in the cards!
For 11001 we have $16+8+0+0+1=25$, so 11001 in binary is equivalent to 25 in decimal.

Applet Instructions:¶

Create a number in binary: clicking on a button with a 0 turns it into a 1.
The corresponding power of 2 below will change colour, and the 0 in front will change to a 1.
The decimal equivalent will appear at the bottom.

%%HTML

<!DOCTYPE html>
<html>
<head>
<meta name="viewport" content="width=device-width, initial-scale=1">
<style>
.button {
  padding: 15px 25px;
  font-size: 24px;
  text-align: center;
  cursor: pointer;
  outline: none;
  color: #fff;
  background-color: #4CAF50;
  border: none;
  border-radius: 15px;
  box-shadow: 0 9px #999;
}

.button:hover {background-color: #3e8e41}

.disabled {
    opacity: 0.6;
    cursor: not-allowed;
}

.button:active {
  background-color: #3e8e41;
  box-shadow: 0 5px #666;
  transform: translateY(4px);
}
               
.txtbox{
        display: block;
        float: left;
        height: 50px;
        width: 50px;
        font-size: 24px;
        }

.new-meows{
   padding: 10px;
   border: 1px solid grey;
   margin : 10px;
   width: 97%;
   display:flex;
 }
               
.divider{
    width:10px;
    height:auto;
    display:inline-block;
}
</style>
</head>
<body>
               

<h3>Enter a binary number</h3><br>

<button id="card1" onclick="myFunction(this.id);myFunction1(this.id, 'Decimal_card_16', 'box1');" class= "button">0</button>
<button id="card2" onclick="myFunction(this.id);myFunction1(this.id,'Decimal_card_8', 'box2' );" class= "button">0</button>
<button id="card3" onclick="myFunction(this.id);myFunction1(this.id,'Decimal_card_4', 'box3');" class= "button">0</button>
<button id="card4" onclick="myFunction(this.id);myFunction1(this.id,'Decimal_card_2', 'box4');" class= "button">0</button>
<button id="card5" onclick="myFunction(this.id);myFunction1(this.id,'Decimal_card_1', 'box5');" class= "button">0</button>
               
<br>
<br>
<h3>Decimal Equivalent of the given binary number</h3>
               
<div class = "new-meows">               
<input type="text" id = "box1" value="0" class ="txtbox" /> <font size="24" style= vertical-align: middle;>  &#215 </font>
<div class="divider"/>
               
<button id="Decimal_card_16" class= "button ">16</button><font size="24">  + </font>
<div class="divider"/>
<input type="text" id = "box2"  value="0" class ="txtbox"  /> <font size="24"> &#215 </font>
<div class="divider"/>              
<button id="Decimal_card_8"  class= "button ">8</button> <font size="24">+</font>
 <div class="divider"/>              
<input type="text" id = "box3" value="0" class ="txtbox"  /> <font size="24"> &#215 </font>
<div class="divider"/>               
<button id="Decimal_card_4"  class= "button ">4</button><font size="24">+</font> 
<div class="divider"/>               
<input type="text" id = "box4" value="0" class ="txtbox"  /> <font size="24"> &#215 </font>
<div class="divider"/>               
<button id="Decimal_card_2"  class= "button ">2</button><font size="24">+</font> 
<div class="divider"/>               
<input type="text"  id = "box5" value="0" class ="txtbox"  /> <font size="24"> &#215 </font>
<div class="divider"/>               
<button id="Decimal_card_1"  class= "button ">1</button><font size="24"> =</font> 
<div class="divider"/>
<input type="text"  id = "box6" value="" class ="txtbox"  />
</div>  
               
               
<script>
function myFunction(clicked_id) {
    var Button_id = document.getElementById(clicked_id);
    if (Button_id.innerHTML === "0") {
        Button_id.innerHTML = "1";
    } else {
        Button_id.innerHTML = "0";
    }
}
</script>

<script>
               
    function setColor(btn, color_id) {
        var Button_id = document.getElementById(btn);
        if (color_id == 1) {
            Button_id.style.backgroundColor = "#FF0000"
            
                    
        }
        else {
            Button_id.style.backgroundColor = "#4CAF50"
            color_id = 0;
            
        }
    }
</script>
               
<script>
    function setValue(box_id, txt_id) {
        
        document.getElementById(box_id).value = "1";
          if (txt_id == 1) {
             document.getElementById(box_id).value = "1";            
                    
        }
        else {
             
            document.getElementById(box_id).value = "0";           
        }
    }
</script>               


<script>
var  value1, value2, value3, value4, value5;
var result = 0;
function myFunction1(clicked_id, decimal_card, txt_box_no) {
    
	//value1 = 0;
	//value2 = 0;
	//value3 = 0;
	//value4 = 0;
	//value5 = 0;
    

    var Button_id = document.getElementById(clicked_id);
    if(clicked_id ==="card1" && Button_id.innerHTML ==="1"){
         value1 = 16;

         result = result + value1;
         setColor(decimal_card, 1);
         setValue(txt_box_no, 1);
      
    }
    else if(clicked_id ==="card1" && Button_id.innerHTML ==="0"){
        result = result - 16;
        value1 = 0;
        setColor(decimal_card, 0);
        setValue(txt_box_no, 0);
    }
    else if(clicked_id ==="card2" && Button_id.innerHTML ==="1"){
        value2 = 8;
        result = result + value2;
        setColor(decimal_card, 1);
        setValue(txt_box_no, 1);
    }
     else if(clicked_id ==="card2" && Button_id.innerHTML ==="0"){
         result = result - 8;
         value2 = 0;
         setColor(decimal_card, 0);
         setValue(txt_box_no, 0);
    }
    else if(clicked_id ==="card3" && Button_id.innerHTML ==="1"){
        
        value3 = 4;
        result = result + value3;
        setColor(decimal_card, 1);
        setValue(txt_box_no, 1);
    }
      else if(clicked_id ==="card3" && Button_id.innerHTML ==="0"){
          
          value3 = 0;
          result = result - 4;
          setColor(decimal_card, 0);
          setValue(txt_box_no, 0);
          
    }
    else if(clicked_id ==="card4" && Button_id.innerHTML ==="1"){
         value4 = 2;
         result = result + value4;
         setColor(decimal_card, 1);
         setValue(txt_box_no, 1);
    }
      else if(clicked_id ==="card4" && Button_id.innerHTML ==="0"){
          value4 = 0;
          result = result - 2;
          setColor(decimal_card, 0);
          setValue(txt_box_no, 0);          
    }
  
    
    else if(clicked_id ==="card5" && Button_id.innerHTML ==="1"){
         value5 = 1;
         result = result + value5;
         setColor(decimal_card, 1);
         setValue(txt_box_no, 1);
    }
     else if(clicked_id ==="card5" && Button_id.innerHTML ==="0"){
         value5 = 0;
         result = result - 1;
         setColor(decimal_card, 0);
         setValue(txt_box_no, 0);
    }
    document.getElementById("Result_of_binary").innerHTML = result;
    document.getElementById("box6").value = result;
   
}



   
</script>   
 

 <h3>The decimal equivalent is: <span id="Result_of_binary"></span></h3>       
</body>
               

              
</html>

Enter a binary number

Decimal Equivalent of the given binary number

×

+

×

+

×

+

×

+

×

=

The decimal equivalent is:

A remark on notation¶

When we’re working with more than one base system at the same time (for example, when converting from decimal to binary) we need a way of specifying what base we’re using.

A common notation is to place the digits in parentheses, with the base as a subscript.
For example, we can write $(10110)_2$ to indicate that we’re expressing a number in binary.

This lets us write equations, like $(10110)_2 = (22)_{10}$, to indicate that we’ve expressed the same number in two different bases.

Some people use notation like $\mathbf{Bin}\,10110 = \mathbf{Dec}\, 22$ instead.
This notation is a little clumsier, but it can be used for a great joke.

Converting Decimal to Binary¶

In the other direction, our goal is to flip the right cards to add up to a given number.
Let’s say we want the binary representation for 13.

We could simply employ trial and error, flipping cards and checking each time to see if we have it right.
This isn’t very efficient though. Instead, let’s think like a computer scientist, and devise an algorithm.

First, we definitely don’t want to add any numbers greater than our number. So 16 is out: we set that card to 0.
Next, we’re going to want the biggest power of 2 that’s less than our number. So 8 is in: we set that card to 1.
Now we ask ourselves, what do we have left to add? This is a subtraction problem! We want 13 and we have 8, so we still have $13-8=5$ left to add.
To continue, we take the value that’s left – 5 – and repeat steps 2 and 3. Since 4 is less than 5, we flip that card to 1, and find the difference: $5-4=1$.
We keep repeating, until there’s nothing left to add. But all we have left is 1, so we flip that card, and we’re done!

Note: the steps we just described give an example of what’s called a recursive algorithm.
In a recursive algorithm, we repeat a series of steps until a desired goal is reached.
Many computer programs employ recursive algorithms to accomplish their task.

Visualizing the Algorithm¶

Instructions:¶

Enter a value for n between 1 and 31 in the input box.
A graph will be generated to show the original numbers as a blue dot.
The red dots will represent the powers of 2 we need to make the remainder 0.
Below the graph, the steps are also shown for further clarification. For Example if the input number is 25, then the steps will be the first step : 25 - 16 = 9 the next step : 9 - 8 = 1 the final step : 1 - 1 = 0

From the steps we know that we need 16, 8, 1 as powers of 2 to make the remainder 0.

So The binary for $(25)_{10}$ is $(11001)_{2}$.

py.init_notebook_mode(connected=True)

def plot_stored_values(store_plot_value, value):
    
    value_list = []
    value_list.append(value)
    
    N = len(store_plot_value)
    random_y = np.zeros(N)        

    # Create a trace
    trace = go.Scatter(
        x = store_plot_value,
        y = random_y,
        marker = dict(color = 'rgb(128, 0, 0)',),
        mode = 'markers',
        name =  "Derived Numbers of power of 2"
     )
    
    trace_value = go.Scatter(
        x = value_list,
        y = [0],
        marker = dict(color = 'rgb(0, 0, 128)',),
        mode = 'markers',
        name = "Original number"
     )

    data = [trace , trace_value]
    layout = go.Layout(
        title ='Decimal Value numbers',
        xaxis =dict(
        title='Decimal Values',
        titlefont=dict(
            family='Courier New, monospace',
            size=18,
            color='#7f7f7f'
            )
        ),
        yaxis=dict(
        title='',
        titlefont=dict(
            family='Courier New, monospace',
            size=18,
            color='#7f7f7f'
            )
        )
    )
    fig = go.Figure(data=data, layout=layout)
    py.iplot(fig, filename='basic-line')

#function for finding the power of 2 
def power_two_1(n):
    return int(math.log(n, 2))

def power_two(x):
    return x.bit_length()-1

#function for calculating the algorithm value
store_plot_value = []
def Calculate_Value(x):
    store_plot_value = []
    
    power_of_2 = power_two(x)
    #print(power_of_2)
    first_value = 2 ** power_of_2
    store_plot_value.append(first_value)
    plot_value = x - 2 ** power_of_2
    
    #store_plot_value.append(plot_value)
    while(plot_value > 0):
        
        power_of_2 = power_two(plot_value)
        #print(power_of_2)
        store_value =  2 ** power_of_2
        store_plot_value.append(store_value)
        plot_value = plot_value - 2 ** power_of_2
       
    #plot_stored_values(store_plot_value)
    return store_plot_value

Algorithm_value = widgets.BoundedIntText(
    value = 0,
    min = 0,
    max = 256,
    step = 1,
    description = 'Enter value:',
    disabled = False
)

def on_value_change(change):
    
    clear_output(wait= False)
    display(Algorithm_value)
    Plot_values = []
    #Calculate_Value(change['new'])
    Plot_values = Calculate_Value(change['new'])
    plot_stored_values(Plot_values, change['new'])
    
    
    visual_value = change['new'] - Plot_values[0]
    
    interim_value = visual_value
    print("the first step : {} - {} = {}".format(change['new'],Plot_values[0], interim_value ))
    
    for i in Plot_values[1:]:
        temp = interim_value
        interim_value = interim_value - i
        print("the next step : {} - {} = {}".format(temp, i , interim_value ))
    print("From the steps we see that we need", Plot_values, " as powers of 2 to make the remainder 0.")

        
display(Algorithm_value)
Algorithm_value.observe(on_value_change, names='value')

Try doing the algorithm yourself!¶

Instructions:¶

Enter a value for n between 1 and 31 in the input box.
When you click on a power of 2, it will be subtracted from your number.
Keep working until the amount r that remains is zero.
Your number in binary will be shown at the bottom.

#ggb.material('VJJpYMQ2').draw()

%%html
<iframe scrolling="no" title="TriangleAnimation" src="https://www.geogebra.org/material/iframe/id/VJJpYMQ2/width/800/height/300/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="716px" height="272px" style="border:0px;"> </iframe>

Practice Questions¶

Now that you’ve seen a few examples, it’s time to try some on your own.
But remember: two problems worth of practice is not enough to master this skill.
Make sure you take the time to work through additional problems from your teacher or textbook.

Convert the following Decimal Numbers to binary¶

Question 1¶

$(57)_{10} = (A)_2$

a = widgets.IntText(value=0, description='A =', disabled=False)

IPython.display.display(a)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(a)
    if a.value == 111001:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

a.observe(check, 'value')

%%html
<html>
<head>
<script type="text/javascript">
<!--
function toggle(id) {
var e = document.getElementById(id);
if(e.style.display == 'none')
e.style.display = 'block';
else
e.style.display = 'none';
}
//-->
</script>
</head>

<body>
<div id="question1">
Solution Question 1.  <button id = "A"
onclick="toggle('answer1');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer1">
As $64(2^6)$ is closest power of 2 for 57, so there will be atleast 6 digits for binary. <br />

the first step : 57 - 32 = 25  <br />
the next step : 25 - 16 = 9  <br />
the next step : 9 - 8 = 1  <br />
the last step : 1 - 1 = 0  <br />
so, the solution is: <br /> $1*32+ 1*16+ 1*8+ 0*4 + 0*2 + 1*1 $= $(111001)_2$
</div>

Solution Question 1. to see the answer.

Question 2¶

$(79)_{10} = (B)_2$

b = widgets.IntText(value=0, description='B =', disabled=False)
IPython.display.display(b)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(b)
    if b.value == 1001111:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

b.observe(check, 'value')

%%html
<html>
<body>
<div id="question2">
Solution Question 2.  <button id = "B"
onclick="toggle('answer2');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer2">
As $128(2^7)$ is closest power of 2 for 79, so there will be atleast 7 digits for binary. <br />

the first step : 79 - 64 = 15 <br />
the next step : 15 - 8 = 7 <br />
the next step : 7 - 4 = 3 <br />
the next step : 3 - 2 = 1 <br />
the last step : 1 - 1 = 0 <br />
so, the solution is: <br /> $1*64+ 0*32+ 0*16+ 1*8+ 1*4 + 1*2 + 1*1 $= $(1001111)_2$
</div>


</body>
</html>

Solution Question 2. to see the answer.

Question 3¶

$(39)_{10} = (C)_2$

c = widgets.IntText(value=0, description='C =', disabled=False)
IPython.display.display(c)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(c)
    if c.value == 100111:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

c.observe(check, 'value')

%%html
<html>
<body>
<div id="question3">
Solution Question 3. <button id = "C"
onclick="toggle('answer3');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer3">
As $64(2^6)$ is closest power of 2 for 39, so there will be atleast 6 digits for binary. <br />
the first step : 39 - 32 = 7 <br />
the next step : 7 - 4 = 3 <br />
the next step : 3 - 2 = 1 <br />
the last step : 1 - 1 = 0 <br />
so, the solution is: <br /> $1*32+ 0*16+ 0*8+ 1*4 + 1*2 + 1*1 $= $(100111)_2$
</div>


</body>
</html>

Solution Question 3. to see the answer.

Convert the following Binary Numbers to Decimal¶

Question 4¶

$(10101)_{2} = (D)_{10}$

d = widgets.IntText(value=0, description='D =', disabled=False)
IPython.display.display(d)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(d)
    if d.value == 21:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

d.observe(check, 'value')

%%html
<html>
<body>
<div id="question4">
Solution Question 4. <button id = "C"
onclick="toggle('answer4');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer4">
As $64(2^6)$ is closest power of 2 for 39, so there will be atleast 6 digits for binary. <br />
the first step : 39 - 32 = 7 <br />
the next step : 7 - 4 = 3 <br />
the next step : 3 - 2 = 1 <br />
the last step : 1 - 1 = 0 <br />
so, the solution is: <br /> $1*32+ 0*16+ 0*8+ 1*4 + 1*2 + 1*1 $= $(100111)_2$
</div>


</body>
</html>

Solution Question 4. to see the answer.

Question 5¶

$(01111)_{2} = (E)_{10}$

e = widgets.IntText(value=0, description='E =', disabled=False)
IPython.display.display(e)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(e)
    if e.value == 15:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

e.observe(check, 'value')

%%html
<html>
<body>
<div id="question5">
Solution Question 5.  <button id = "D"
onclick="toggle('answer5');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer5">
$(10101)_2 = 1 * 2^{4} + 0 * 2^{3} + 1 * 2^{2} + 0* 2{1} + 1*2{0}$ <br />  &emsp; &emsp; &emsp; &emsp;
           = $1*16+ 0*8+ 1*4 + 0*2 + 1*1$ <br /> &emsp; &emsp; &emsp; &emsp;
           = $(21)_{10}$ <br />

</div>

</body>
</html>

Solution Question 5. to see the answer.

Question 6¶

$(100100)_{2} = (F)_{10}$

f = widgets.IntText(value=0, description='F =', disabled=False)
IPython.display.display(f)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(f)
    if f.value == 36:
        print("That's right! Great work!")
    else:
        print("Sorry, try again or practice some more using the tools above")

f.observe(check, 'value')

%%html
<html>
<body>
<div id="question6">
Solution Question 6. <button id = "D"
onclick="toggle('answer6');">Click Here</button> to see the answer.
</div>
<div style="display:none" id="answer6">
$(100100)_2 = 1 * 2^{5} + 0 * 2^{4} + 0 * 2^{3} + 1 * 2^{2} + 0* 2{1} + 1*2{0}$ <br />  &emsp; &emsp; &emsp; &emsp;
           = $1*32+ 0*16+ 0*8+ 1*4 + 0*2 + 0*1$ <br /> &emsp; &emsp; &emsp; &emsp;
           = $(36)_{10}$
</div>

</body>
</html>

Solution Question 6. to see the answer.

Conclusion¶

There are many different ways to represent the numbers we use every day.
The best way of representing a number can depend on what we’re trying to do.

Digital computers typically use two states rather than more because:

It is usually easy to distinguish two states;
Two is enough to represent anything you like as a sequence of bits; and
Computers don’t mind long sequences.

Since we live in a digital era surrounded by machines, we must learn how machines understand the living world.

Approximating Square Roots of Non-Perfect Squares Budget and Banking

Callysto Curriculum Notebooks

Binary decimal conversion¶

Introduction¶

Big Ideas¶

Background information¶

Numeral systems¶

Why Binary?¶

Base and Digits in a Positional System¶

An answer to an impractical problem.¶

Counting in binary¶

Converting between decimal and binary notation.¶

Converting binary to decimal¶

Example:¶

Interactive Method¶

Applet Instructions:¶

Enter a binary number

Decimal Equivalent of the given binary number

The decimal equivalent is:

A remark on notation¶

Converting Decimal to Binary¶

Visualizing the Algorithm¶

Instructions:¶

Try doing the algorithm yourself!¶

Instructions:¶

Practice Questions¶

Convert the following Decimal Numbers to binary¶

Question 1¶

Question 2¶

Question 3¶

Convert the following Binary Numbers to Decimal¶

Question 4¶

Question 5¶

Question 6¶

Conclusion¶