
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
The raw code for this IPython notebook is by default hidden for easier reading.
To toggle on/off the raw code, click <a href="javascript:code_toggle()">here</a>.''')
%%html
<style>
.output_wrapper button.btn.btn-default,
.output_wrapper .ui-dialog-titlebar {
display: none;
}
</style>
Shape and Space: Geometry¶
import matplotlib.pyplot as plt
import ipywidgets
from ipywidgets import widgets, interact, interact_manual, Button, Layout
from IPython.display import Javascript, display
Geometry is one of the most valuable topics of everyday life. It is important for driving, cooking, drawing, decorating, and so many other tasks. It is also instinctive to human beings. Even babies use geometry when deciding that circular pieces fit in circular holes. So, this notebook is describing the math behind natural activities.
In this notebook, you will learn how to define and explain length, width. You will also learn how to explain height, depth, thickness, perimeter and circumference. This notebook will help introduce and explain the metric units. These topics will be taught through visual aids and interactive models.
Background On Shapes¶
To start describing geometric shapes, we will first have to decide in which way the shapes appear:
Two Dimensions¶
In this case, objects appear flat. The following shapes illustrate this idea:

While these objects may seem very simple, they are a good way to introduce length, width, perimeter, and circumference.
Length and Width¶
The length of some rectangle is the longest side, (Or edge), of it. But, the width, is the shortest side of a rectangle. A useful way to remember this is to think of Length as Long.
We can label the rectangular shape with its length and width:
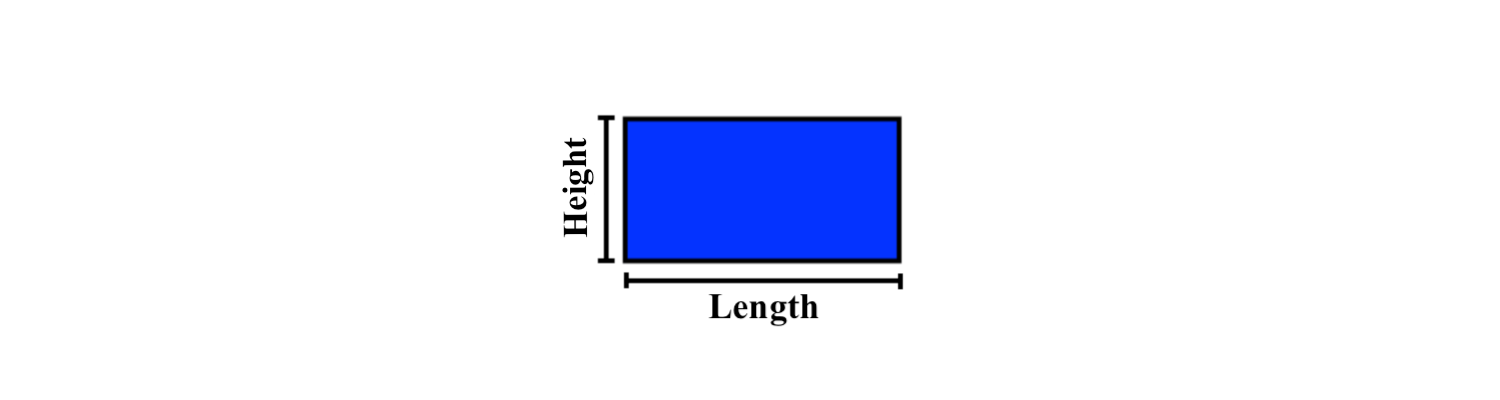
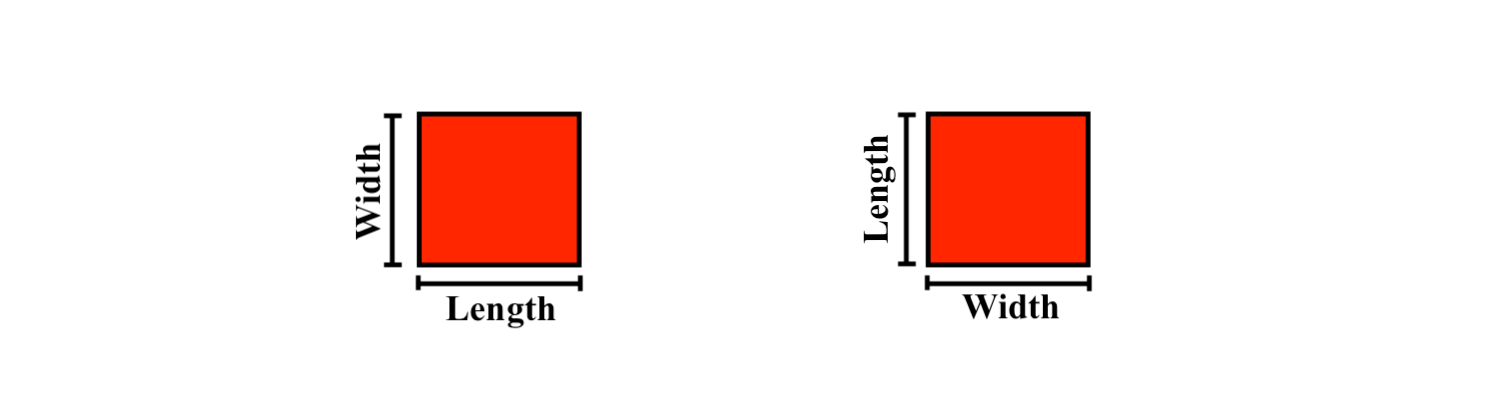
Now, you may be wondering, “How do we fill out the length and width of a square, where all sides are equal?” Because all sides are equal, this means that length and width are interchangeable. So ,we can have either of the following:
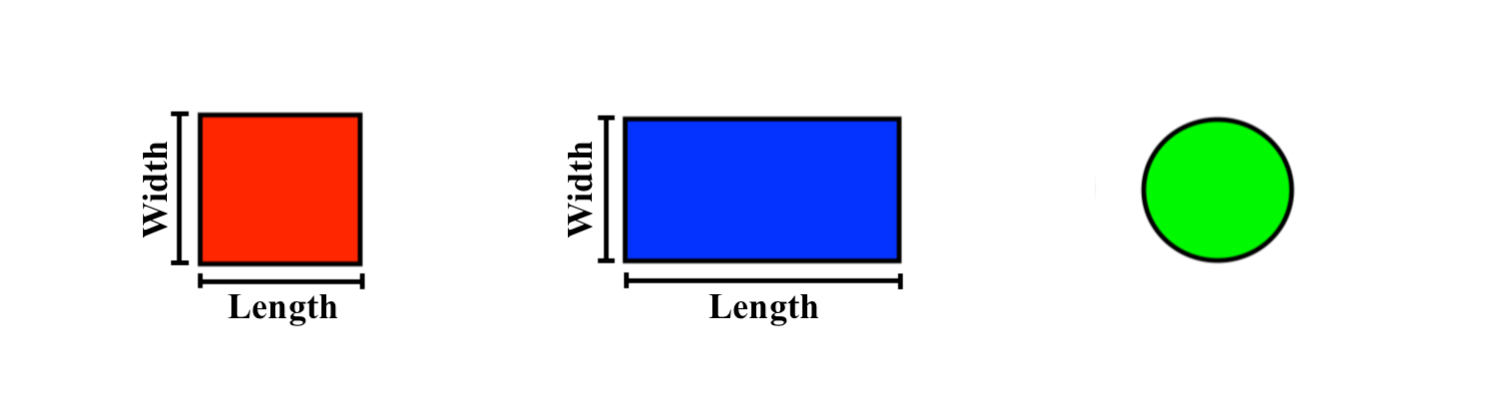
Thus, we’ve found the width and length of all the rectangular shapes:
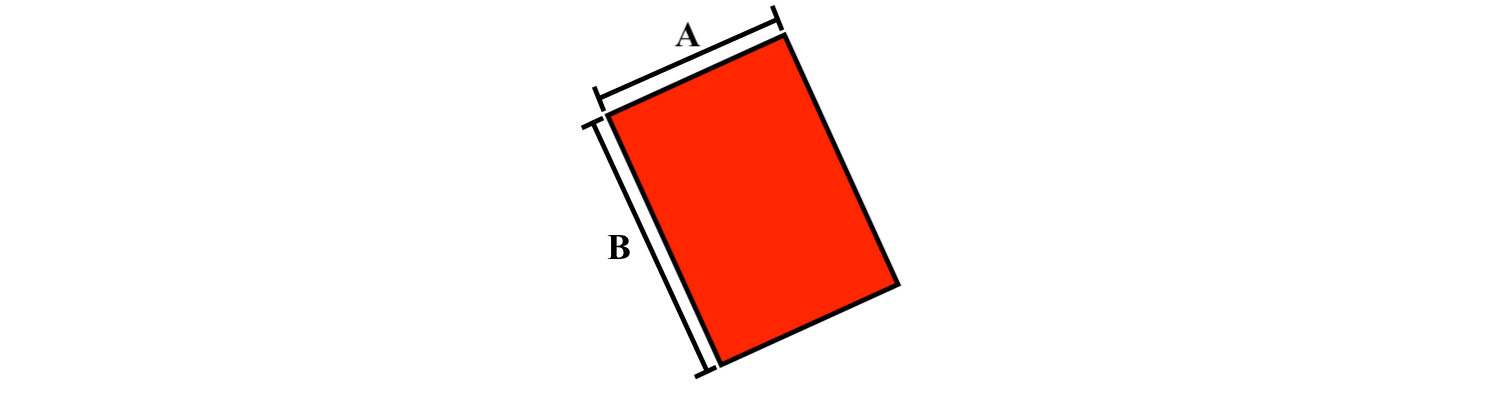
Practice Question 1¶
Given the following rectangle:
from ipywidgets import interact_manual,widgets
print("In the picture above, which edge is the width?")
@interact(answer =widgets.RadioButtons(
options=["A", "B"],
value=None,
description="Answer: ",
disabled=False
))
def reflective_angle_question(answer):
if answer=="A":
print("Correct!\
\nThe width is the shortest side of this rectangle.")
elif answer =="B":
print("Incorrect.\
\nRemember, the width of a rectangle depends on its orientation.")
In the picture above, which edge is the width?
Perimeter¶
With this information we can now find the perimeter of a rectangle or square. The perimeter is the total length of all sides of a rectangular shape.
To find the perimeter of a rectangle, one must add all the sides together. The formula for the perimeter of a rectangle is given by
But, since we know that:
And that:
We can simplify the formula to look like:
Now, we have a simplified formula for finding the perimeter of any rectangle.
Finding the perimeter of any square is even simpler since we know that all sides have equal length. So, the formula is even simpler. You can either write:
Or:
Practice Question 2¶
Given the following rectangle:
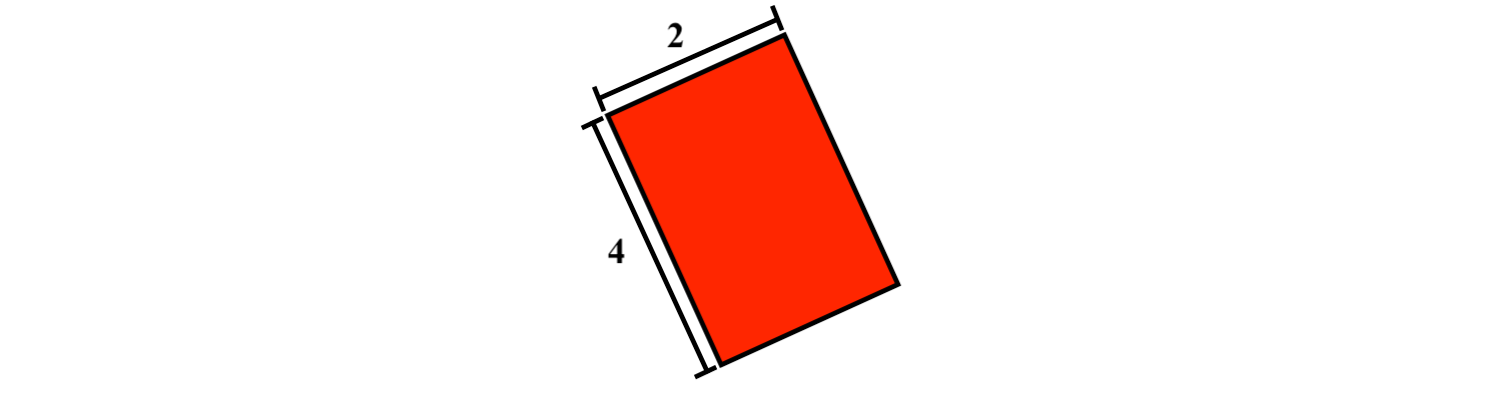
from ipywidgets import interact_manual,widgets
print("What is the perimeter?")
@interact(answer = widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "12":
print("Correct!\
\nThe perimeter is 2*(2) + 2*(4), which equals 12.")
elif answer == "":
print("Type the perimeter of the rectangle.")
else:
print("Incorrect.\
\nRemember, the formula for calulating the perimeter is 2*(width) + 2*(length).")
What is the perimeter?
Diameter And Radius¶
So far we’ve been focusing on rectangular objects, but now we must focus on circular shapes. We should know some useful facts about circles already, like how to find the diameter and radius, but we’ll do a quick refresher on the subject.
To find either of these values, we begin by locating the exact middle of the circle.

Next, if we drew a straight line from the middle to an edge of the circle, we’d get the radius:
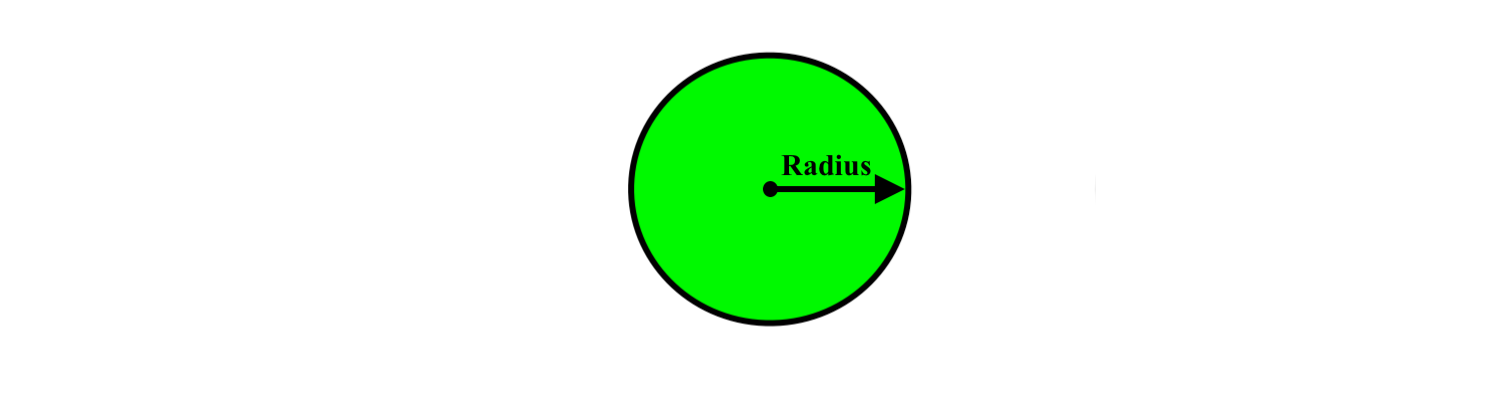
We get the diameter if we draw a line starting from any edge of the circle to the middle, and then to another edge:
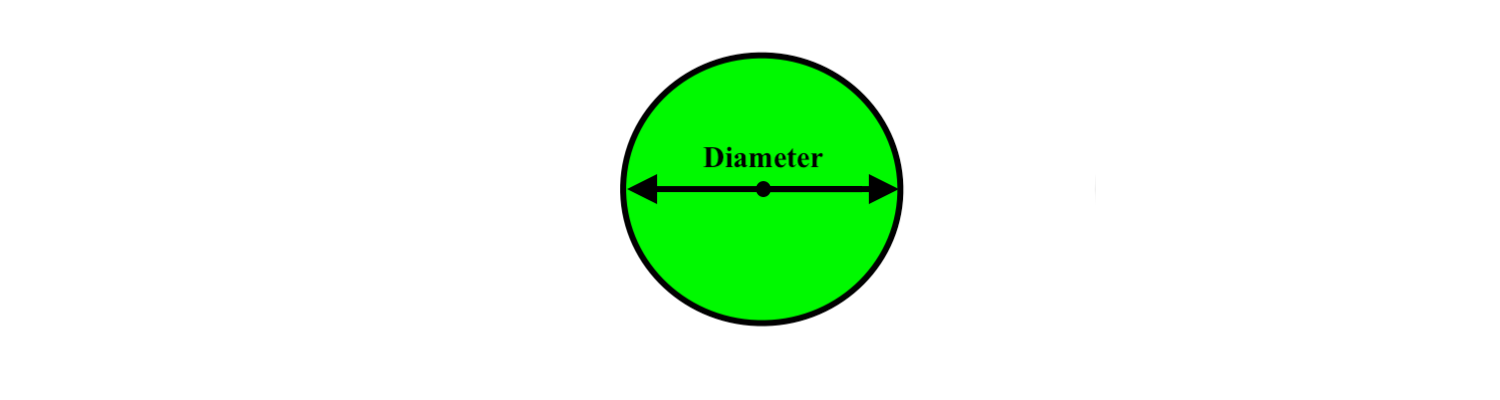
It is also important to note that the radius of any circle is half the size of the diameter:
You can think of the diameter as being twice the radius.
Circumference¶
Now that we’ve found the radius and the diameter, we can begin to look at how to find the circumference of the circle.
First, we will define what the circumference actually is. The circumference is the total length around the circle:

To find the circumference of any circle, we first have to find either the radius or the diameter. Then, we can use either of the following formulas to calculate the circumference.
If we only have the radius, we can use the following formula to calculate the circumference:
If we only have the diameter, we can use the following formula to calculate the circumference:
Now we have a formula we can use to calculate the circumference of a circle!
Practice Question 3¶
Given the following circle:
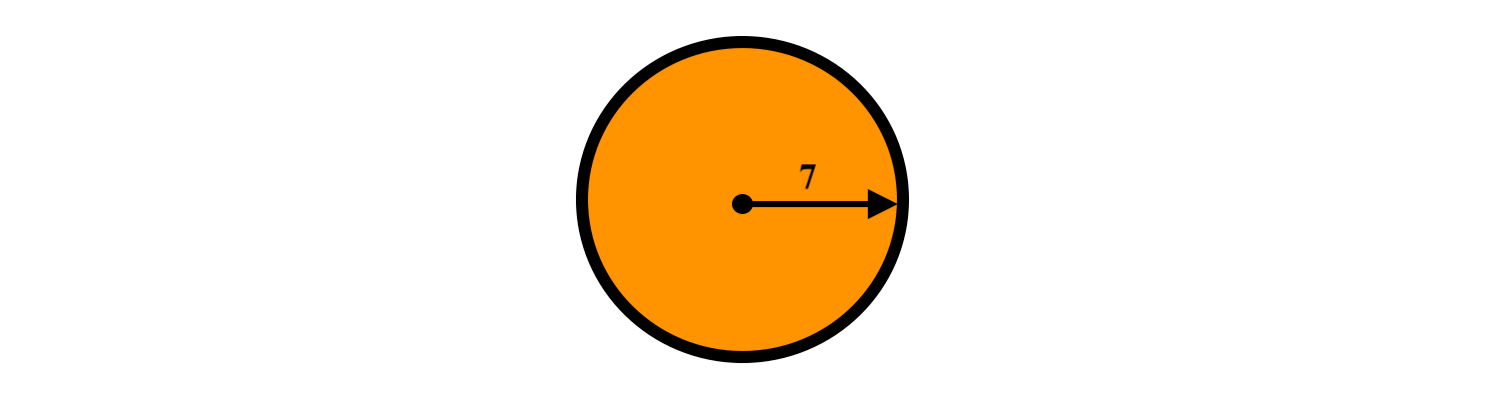
from ipywidgets import interact_manual,widgets
print("What is the circumference? (Round to the nearest whole number)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "44":
print("Correct!\
\nThe circumference is 2 * pi * (7). This equals 43.982297... which is rounded to 44.")
elif answer == "":
print("Type the circumference of the circle.")
else:
print("Incorrect.\
\nRemember, we are only given the radius here.")
What is the circumference? (Round to the nearest whole number)
Three Dimensions¶
In three dimensions objects appear to have depth. Suppose you are looking at the following rectangle from the black circle:
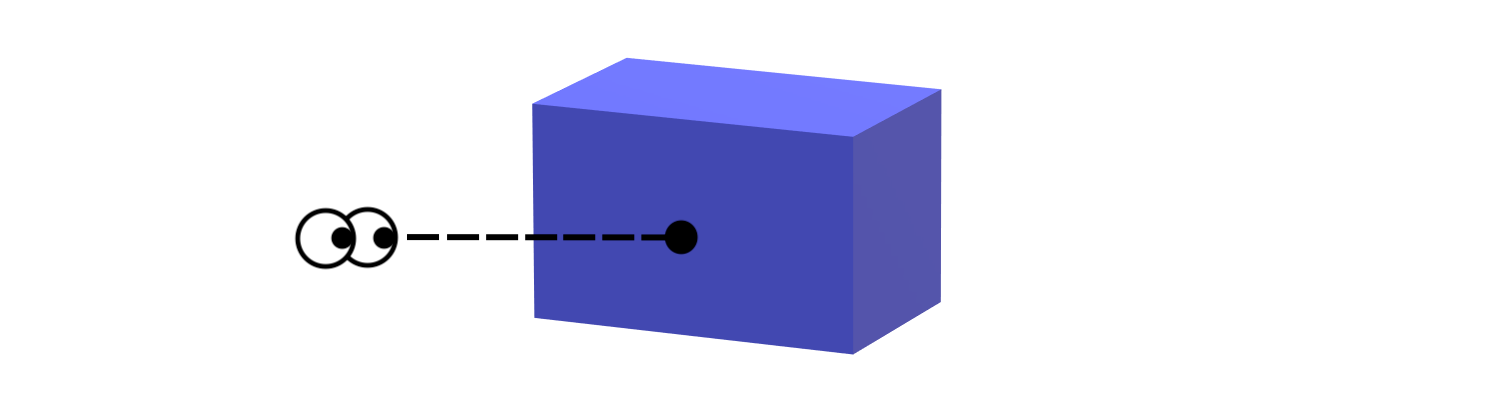
One can see that a 3 dimensional rectangle has many more unique edges than a 2 dimensional one. To account for these changes humans came up with new terms to help describe these shapes.
Height¶
The height of a rectangle helps describe how tall some object is. This is the edge that goes vertically from the top of the shape to the bottom. A useful way to remember this is to think height is for tall.
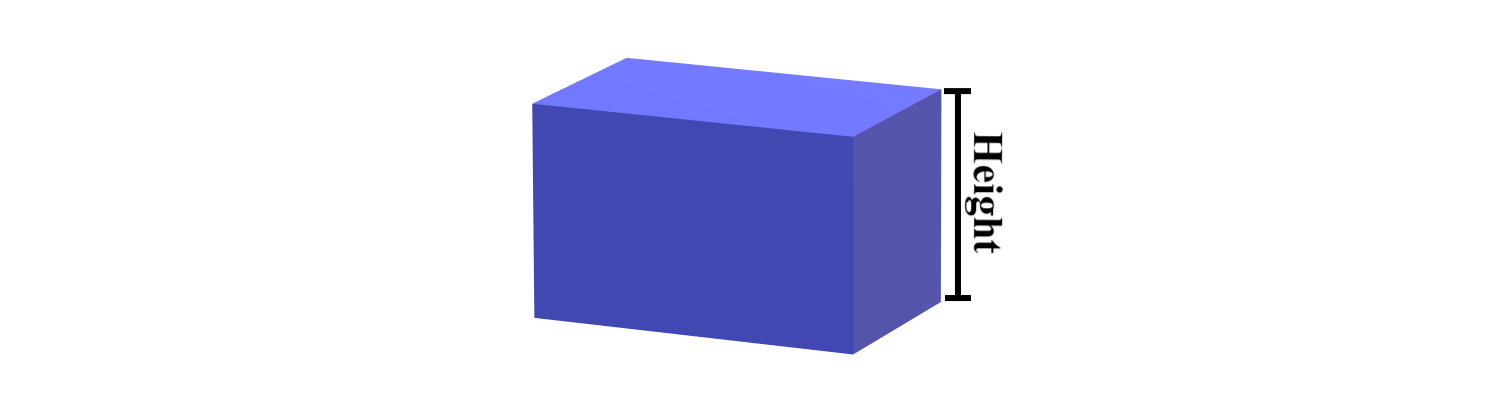
We can also find the height of a 2 dimensional shape:

Depth¶
The depth of a rectangle is how deep an object goes in. This is the edge that goes away from you. A useful way to remember this is to to think depth is for deep.
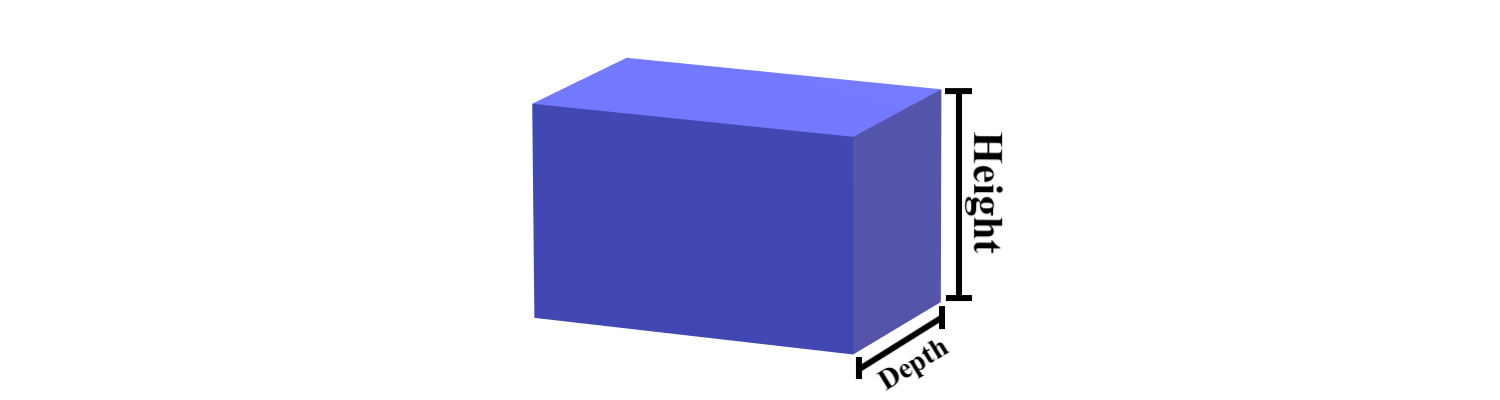
Width¶
The width of a 3 dimensional rectangle is the edge that’s facing you. It’s usually the one directly at the bottom of where you’re facing.
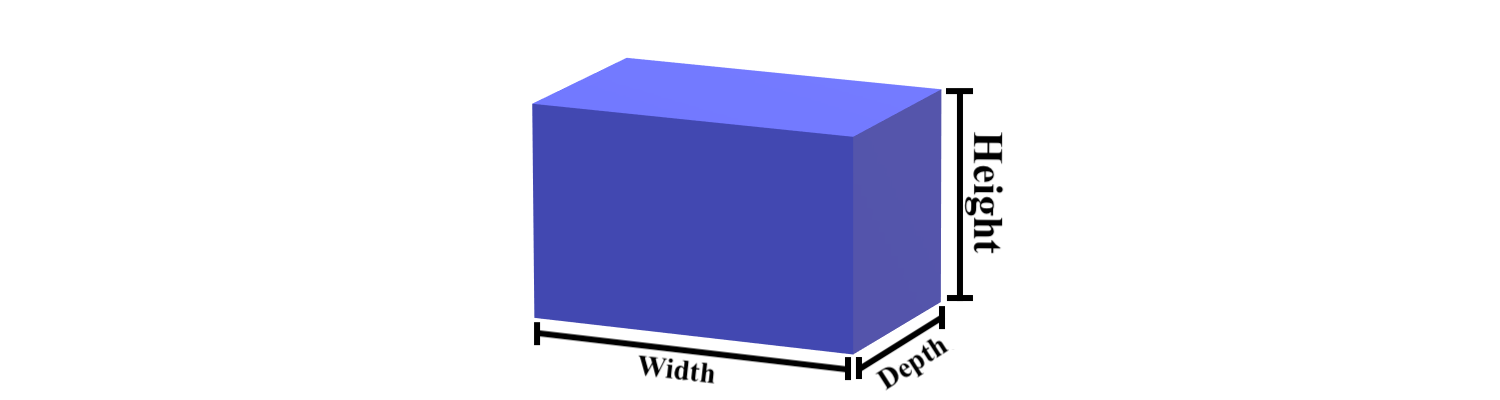
Thickness¶
The thickness of a 3 dimensional shape is how deep some face of the shape is. A good way to picture this is to think about the walls of your house. The distance between the inside wall and the outer wall is the thickness of your house. This idea can be applied to all types of boxes and shapes, even lines:

Cube¶
As you may have guessed, the process of deciding height, depth, thickness, and width is the same for a cube:
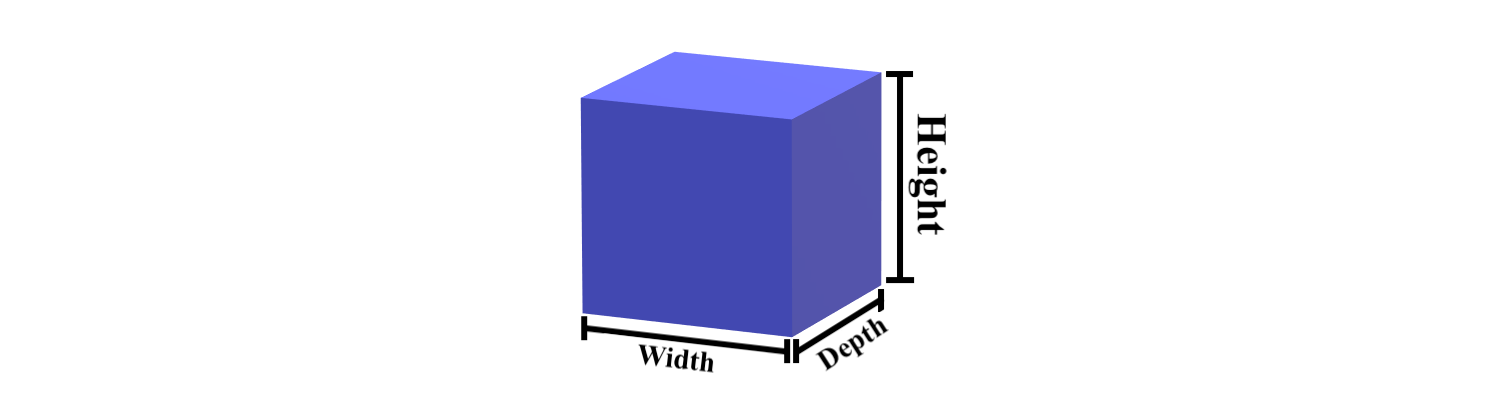
The only difference here is that the length of every edge is the same.
Practice Question 4¶
You view the following rectangle from the black circle:
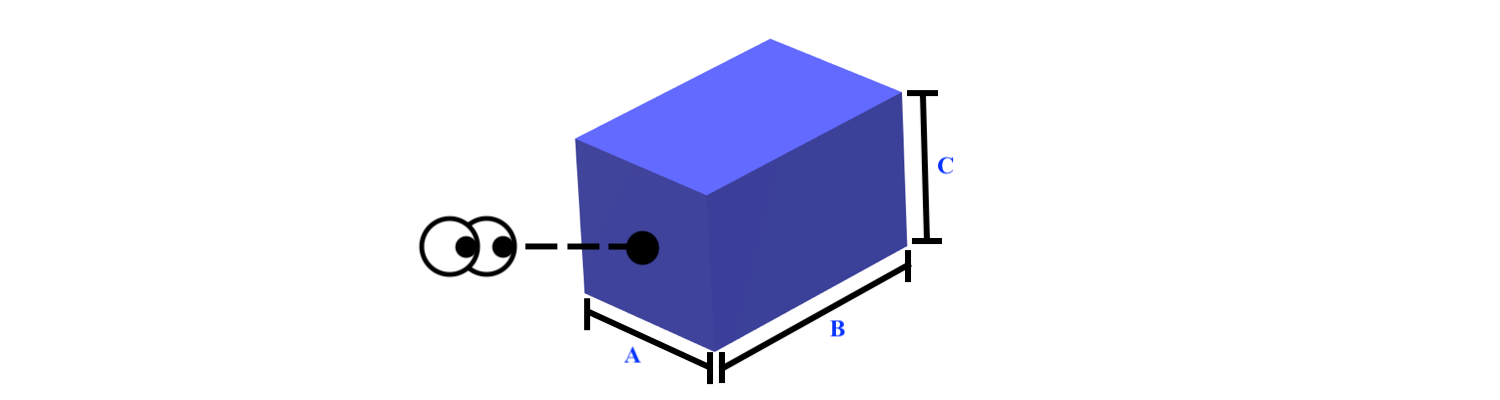
from ipywidgets import interact_manual,widgets
print("Which edge is the depth?")
@interact(answer =widgets.RadioButtons(
options=["A", "B", "C"],
value=None,
description="Answer: ",
disabled=False
))
def reflective_angle_question(answer):
if answer=="A":
print("Incorrect.\
\nRemember, the depth is how deep, or far back an object goes, from your perspective.")
elif answer =="B":
print("Correct!\
\nThe depth is how deep, or far back an object goes, from your perspective.")
elif answer =="C":
print("Incorrect.\
\nRemember, the depth is how deep, or far back an object goes, from your perspective.")
Which edge is the depth?
from ipywidgets import interact_manual,widgets
print("Which edge is the height?")
@interact(answer =widgets.RadioButtons(
options=["A", "B", "C"],
value=None,
description="Answer: ",
disabled=False
))
def reflective_angle_question(answer):
if answer=="A":
print("Incorrect.\
\nRemember, the height is the edge that goes vertically, or top to bottom.")
elif answer =="B":
print("Incorrect.\
\nRemember, the height is the edge that goes vertically, or top to bottom.")
elif answer =="C":
print("Correct!\
\nThe height is the side that goes from top to bottom.")
Which edge is the height?
from ipywidgets import interact_manual,widgets
print("Which edge is the width?")
@interact(answer =widgets.RadioButtons(
options=["A", "B", "C"],
value=None,
description="Answer: ",
disabled=False
))
def reflective_angle_question(answer):
if answer=="A":
print("Correct!\
\nThe width is the edge of the object that is closest to you, from your perspective.")
elif answer =="B":
print("Incorrect.\
\nRemember, the width is the edge of the object that is closest to you, from your perspective.")
elif answer =="C":
print("Incorrect.\
\nRemember, the width is the edge of the object that is closest to you, from your perspective.")
Which edge is the width?
Measurements¶
The last topic we will introduce in this section is the topic of measurements.
This topic is important to every day life as it simplifies a lot of human activities. Think about the length of one of your nails. That length can’t be treated the same way as the length it takes to go to the Moon from Earth. In other, ‘mathier’, words, we can’t calculate long distances using the same methods we calculate small ones. Otherwise we’d get huge numbers for the long stuff, or tiny ones for the small stuff.
So, humans came up with a way to solve this problem, and they created the metric units. These metric units help to calculate lengths. There are 7 of these units we need to focus on: Kilometres, hectometres, decametres, metres, decimetres, centimetres, and millimetres.
While this may seem like a lot of units to memorize, they’ll become very intuitive by the end of this lesson.
The following is a diagram of how these units all interact together. It shows what 1 metre would look like in each of the units. Make sure to take your time studying it.
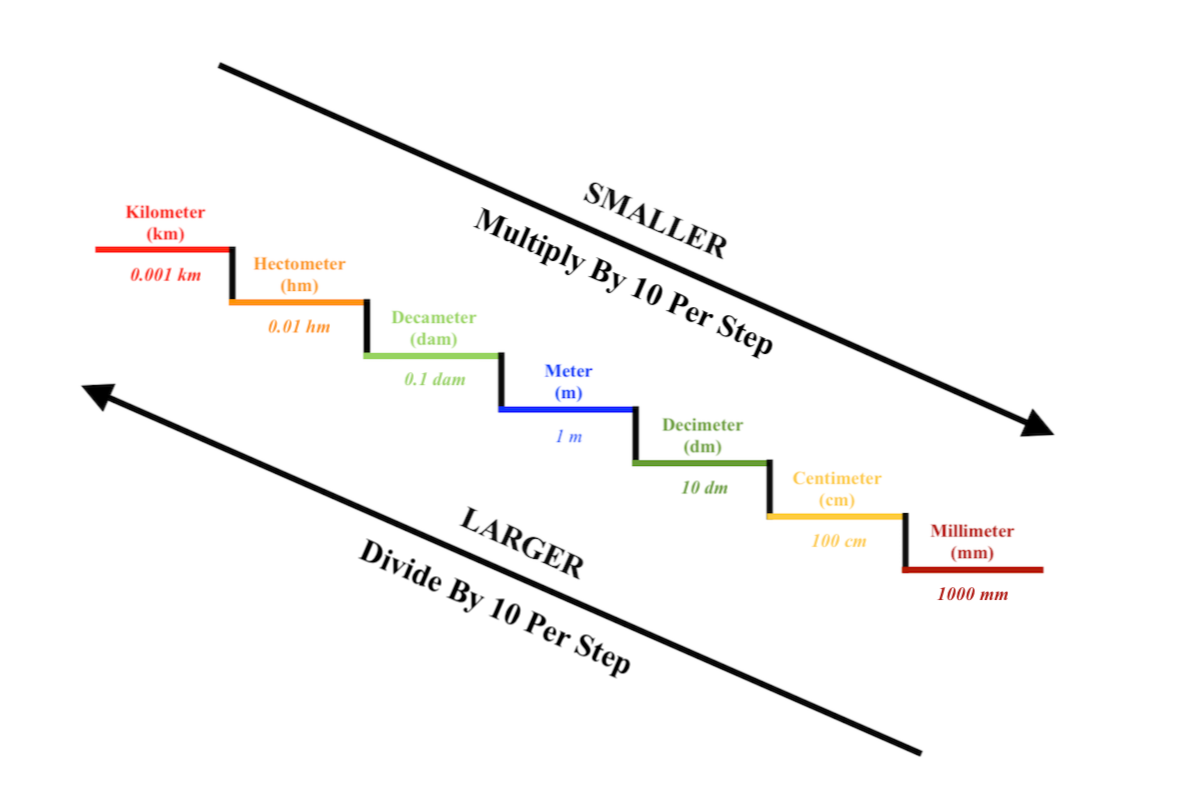
As you may be able to tell from the diagram, these units interact with each other in a special way. This concept is explained in the following two ways:
GOING UP each step is 10 times BIGGER than the last step: This means that each time you go up a step, your measurement becomes longer. For example, 10 metres, (m), is equal to 1 decametre, (dam). So, each time you go up a step, you must divide by 10.
GOING DOWN each step is 10 times SMALLER than the last step: This means that each time you go down a step, your measurement becomes smaller. For example, 1 metre, (m), is equal to 10 decimetres, (dm). So, each time you go down a step, you must multiply by 10.
So, try to remember: Going down is multiply, Going up is divide.
An Useful Way To Memorize¶
We can use a phrase to help remember each of the measurements and where they go on the stairs is:
“King Henry Died By Drinking Chocolate Milk.”
Then, we know that:
King is for Kilometres.
Henry is for Hectometres.
Died is for Decametres.
By is for Base or Metres.
Drinking is for Decimetres.
Chocolate is for Centimetres.
Milk is for Millimetres.
Some Example Questions¶
Suppose you had 5 decametres, (dam), and you wanted to turn them into kilometres, (km). We know that going from decametres to kilometres is going UP 2 steps, so we must divide the amount of hectometres by 10 twice. This is because:
And:
Then, we can find the answer by writing:
So:
ANSWER: 5 dam = 0.05 km.
Suppose instead that you had 7 centimetres, (cm), and you wanted to turn them into millimetres, (mm). We know that going from centimetres to milimetres is going DOWN 1 step, so we must multiply the amount of centimetres by 10 once. This is because:
Then, we can find the answer by doing:
ANSWER: 7 cm = 70 mm
Practice Question 5¶
Please answer the following true or false questions.
print("True or False: 33 decimetres greater than 0.032 decametres.")
@interact(answer = widgets.RadioButtons(
options=['True', 'False'],
description='Answer:',
value = None,
disabled=False
))
def reflective_angle_question(answer):
if answer=="True":
print("Correct!\
\n33 decimetres is 0.33 decametres, which is greater than the 0.032 decametres.")
elif answer =="False":
print("Incorrect.\
\nRemember, going from decimetres to decametres is going up 2 steps.")
True or False: 33 decimetres greater than 0.032 decametres.
print("True or False: 0.4 hectometres greater than 43 metres.")
@interact(answer = widgets.RadioButtons(
options=['True', 'False'],
description='Answer:',
value = None,
disabled=False
))
def reflective_angle_question(answer):
if answer=="True":
print("Incorrect.\
\nRemember, going from hectometres to metres is going down 2 steps.")
elif answer =="False":
print("Correct!\
\n0.4 decimetres is 40 metres, which is less than the 43 metres.")
True or False: 0.4 hectometres greater than 43 metres.
print("True or False: 3852 milimetres greater than 30 metres.")
@interact(answer = widgets.RadioButtons(
options=['True', 'False'],
description='Answer:',
value = None,
disabled=False
))
def reflective_angle_question(answer):
if answer=="True":
print("Incorrect.\
\nRemember, going from milimetres to metres is going up 3 steps.")
elif answer =="False":
print("Correct!\
\n3852 milimetres is 3.852 metres, which is less than the 30 metres.")
True or False: 3852 milimetres greater than 30 metres.
Practice Question 6¶
The average conventional freight trains in the US are about 2 kilometres long.
from ipywidgets import interact_manual,widgets
print("How long would the train be in metres?")
@interact(answer = widgets.Text(
placeholder = "Enter your number here",
description = 'Answer: ',
disabled = False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "2000":
print("Correct!\
\nThe train is 2 kilometres long, and going from kilometres to metres is going down 4 steps. \
\nThen, we do 2 * 10 * 10 * 10. This equals 2000 metres")
elif answer == "":
print("Type the length of the train in metres.")
else:
print("Incorrect.\
\nRemember, going from kilometres to metres is going down 4 steps.")
How long would the train be in metres?
from ipywidgets import interact_manual,widgets
print("How long would the train be in decametres?")
@interact(answer = widgets.Text(
placeholder = "Enter your number here",
description = 'Answer: ',
disabled = False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "200":
print("Correct\
\nThe train is 2 kilometres long, and going from kilometres to decametres is going down 2 steps. \
\nThen, we do 2 * 10 * 10. This equals 200 decametres.")
elif answer == "":
print("Type the length of the train in decametres.")
else:
print("Incorrect.\
\nRemember, going from kilometres to decametres is going down 2 steps.")
How long would the train be in decametres?
Calculator For Measurements¶
The following is an interactive calculator for going from any of the 7 units to another unit:
from ipywidgets import interact_manual,widgets
from IPython.display import display
#List of all possible measurement types.
MeasureList = ['Kilometres', 'Hectometres', 'Decametres', 'Metres', \
'Decimetres', 'Centimetres', 'Millimetres']
#Used to ensure the description text doesn't get cut off.
style = {'description_width': 'initial'}
#Let user choose the final measurement.
#Bounded between 0 and 9999 to make sure it's positive.
initVal = widgets.BoundedFloatText(value = 0, \
min = 0, \
max = 9999, \
description = 'Measurement Value:', \
style = style)
#Let user choose the initial measurement.
initMeas = widgets.SelectionSlider(options = MeasureList, \
value = 'Kilometres', \
description = 'Initial Measurement:', \
style = style)
#Let user choose the final measurement.
finMeas = widgets.SelectionSlider(options = MeasureList, \
value = 'Kilometres', \
description = 'Final Measurement:', \
style = style)
#Displaying all the previously created widgets in order.
display(initVal)
display(initMeas)
display(finMeas)
from ipywidgets import interact_manual,widgets
from IPython.display import display
import decimal
#"MeasureDict" assigns a numeric value to each of the units of measurement. This will help us to calculate
# going from one unit to another.
MeasureDict = {'Kilometres' : 7, 'Hectometres': 6, 'Decametres': 5,\
'Metres': 4, 'Decimetres': 3, 'Centimetres': 2, 'Millimetres': 1}
#"calculate_final" will determine what the final value obtained from the new measurement type.
def calculate_final(initV, initM, finM):
#Create the global value finV. This will store the final measurement value.
global finV
#Find the difference, (diff), between initM and finM and store it in diff. Two cases exist:
# 1. diff is less than or equal to 0:
# In this case the final measurement type is smaller than or equal to the initial measurement type.
# Therefore, must divide by 10 |diff| amount of times, (Or simply multiply 10 ** diff)
#
# 2. diff is greater than 0:
# In this case the final measurement type is greater than or equal to the final measurement type.
# Therefore, must multiply by 10 diff amount of times, (Or simply multiply 10 ** diff)
#
#Thus, we can use 10**diff as it works for both cases.
diff = initM - finM
finV = initV * 10**diff
#Create a button to calculate the change in measurement.
button = widgets.Button(description="Calculate")
display(button)
def on_button_clicked(b):
#Get the initial value inputed as an integer.
initV = initVal.value
#Get the initial measurement inputed as a string.
initM = initMeas.value
#Get the final measurement inputed as a string.
finM = finMeas.value
#Get the key value of the initial measurement type.
initMeasKey = MeasureDict.get(initM)
#Get the key value of the final measurement type.
finMeasKey = MeasureDict.get(finM)
#Calculate the final value.
calculate_final(initV, initMeasKey, finMeasKey)
#Since after 4 decimal places python begins to use scientific notation, checkFp will be the final value
# rounded to the last 4 decimal places.
checkFp = float(format(finV, '.4f'))
#If the value of checkFp is equal to finV, then simply print out the value of finV.
if (checkFp - finV) == 0:
print("Your initial measurement of " + str(initV) + " " + initM + \
" becomes " + str(finV) + " " + finM + ".")
#Otherwise, if the value of checkFp is not equal to finV, then print the value of finV rounded to the 6th
# decimal place.
else:
print("Your initial measurement of " + str(initV) + " " + initM + \
" becomes " + format(finV, ',.6f') + " " + finM + ".")
button.on_click(on_button_clicked)
Exercises
Question 1¶
Given the following circle:

from ipywidgets import interact_manual,widgets
print("What is the radius? (Round to the nearest CENTIMETRE)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "3":
print("Correct!\
\nThe radius is 19 ÷ (2 * pi). This equals 3.02394... cm which is rounded to 3 cm.")
elif answer == "":
print("Type the radius of the circle.")
else:
print("Incorrect.\
\nRemember, in this question we are given the circumference. \
\nTry to find a way to go from circumference to radius.")
What is the radius? (Round to the nearest CENTIMETRE)
from ipywidgets import interact_manual,widgets
print("What is the diameter? (Round to the nearest METRE)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description = 'Answer: ',
disabled = False
))
def reflective_angle_question(answer):
answer = answer.replace(" " , "")
if answer == "0.06":
print("Correct!\
\nThe diameter is twice the radius, which we found to be 3cm in the last question. \
\nThen, we divide the diameter by 100 to get it to 0.06m.")
elif answer == "":
print("Type the diameter of the circle.")
else:
print("Incorrect.\
\nRemember, in this question we want the nearest metre. \
\nTry using the relationship between radius and diameter.")
What is the diameter? (Round to the nearest METRE)
Question 2¶
Bob is a farmer who built a perfectly square fence that had a perimeter of 32 metres. Suppose that Bob wanted to build the largest circular fence he could inside the square fence.
from ipywidgets import interact_manual,widgets
print("What is the circumference of the circular fence? (Round to the nearest METRE)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "25":
print("Correct!\
\nThe diameter of the new fence would be 32 ÷ 4, which equals 8. \
\nThen, the circumference is 8 * pi. This equals 25.13274...m, or 25m.")
elif answer == "":
print("Type the circumference of the circle.")
else:
print("Incorrect.\
\nRemember, in this question we are given the perimeter of a square fence. \
\nTry finding how long the edge of the square fence is, and then use that as the diameter for the new fence.")
What is the circumference of the circular fence? (Round to the nearest METRE)
Question 3¶
You view the following rectangle from the black circle:
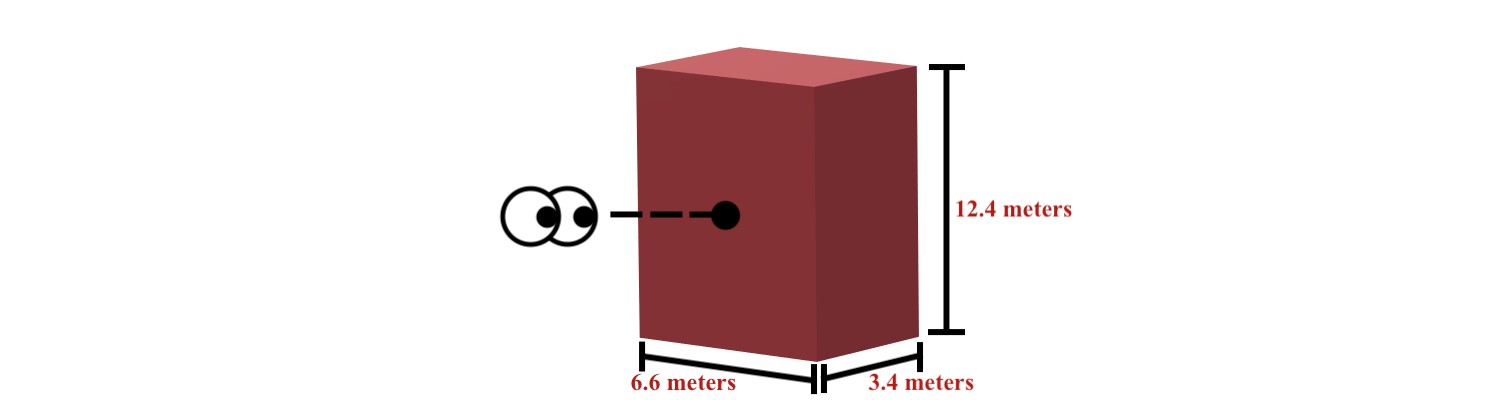
from ipywidgets import interact_manual,widgets
print("What is the height of the rectangle? (Give the value in DECAMETRES)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "1.24":
print("Correct!\
\nThe height is equal to 12.4 metres. \
\nThen, we divide the height by 10 to get 1.24 decametres.")
elif answer == "":
print("Type the height of the rectangle.")
else:
print("Incorrect.\
\nRemember, in this question we want the value in decametres. \
\nTry using the length to the from the bottom to the top of the rectangle.")
What is the height of the rectangle? (Give the value in DECAMETRES)
from ipywidgets import interact_manual,widgets
print("What is the width of the rectangle? (Give the value in CENTIMETRES)")
@interact(answer =widgets.Text(
placeholder = "Enter your number here",
description='Answer: ',
disabled=False
))
def reflective_angle_question(answer):
answer = answer.replace(" ", "")
if answer == "660":
print("Correct!\
\nThe width is equal to 6.6 metres. \
\nThen, we multiply the width by 100 to get 660 centimetres.")
elif answer == "":
print("Type the width of the rectangle.")
else:
print("Incorrect.\
\nRemember, in this question we want the value in centimetres. \
\nTry using the length at the bottom of the rectangle.")
What is the width of the rectangle? (Give the value in CENTIMETRES)
from ipywidgets import interact_manual,widgets
print("What is the depth of the rectangle? (Give the value in HECTOMETRES)")
@interact(answer = widgets.Text(
placeholder = "Enter your number here",
description= 'Answer: ',
disabled= False
))
def reflective_angle_question(answer):
answer = answer.replace(" " , "")
if answer == "0.034":
print("Correct!\
\nThe depth is equal to 3.4 metres. \
\nThen, we divide the depth by 100 to get 0.034 hectometres.")
elif answer == "":
print("Type the width of the rectangle.")
else:
print("Incorrect.\
\nRemember, in this question we want the value in hectometres. \
\nTry using the length at the side of the rectangle.")
What is the depth of the rectangle? (Give the value in HECTOMETRES)
Summary
You will now know how to find length, width, perimeter and circumference. Additionally, you will know how to find height, depth, and thickness. You have also been introduced to the metric units, and how to use them.

