Pythagorean Theorem¶

This notebook will cover the Pythagorean theorem, including its applications and a proof of the theorem.

Note: You should have a solid understanding of square roots and squaring numbers before moving on to this notebook. This notebook assumes you know these concepts, though it also gives more practice of these concepts.

Introduction¶

Say you have 2 sides of a right angle triangle and are trying to figure out the third. How can we do this? Thankfully that’s where the Pythagorean theorem comes in!

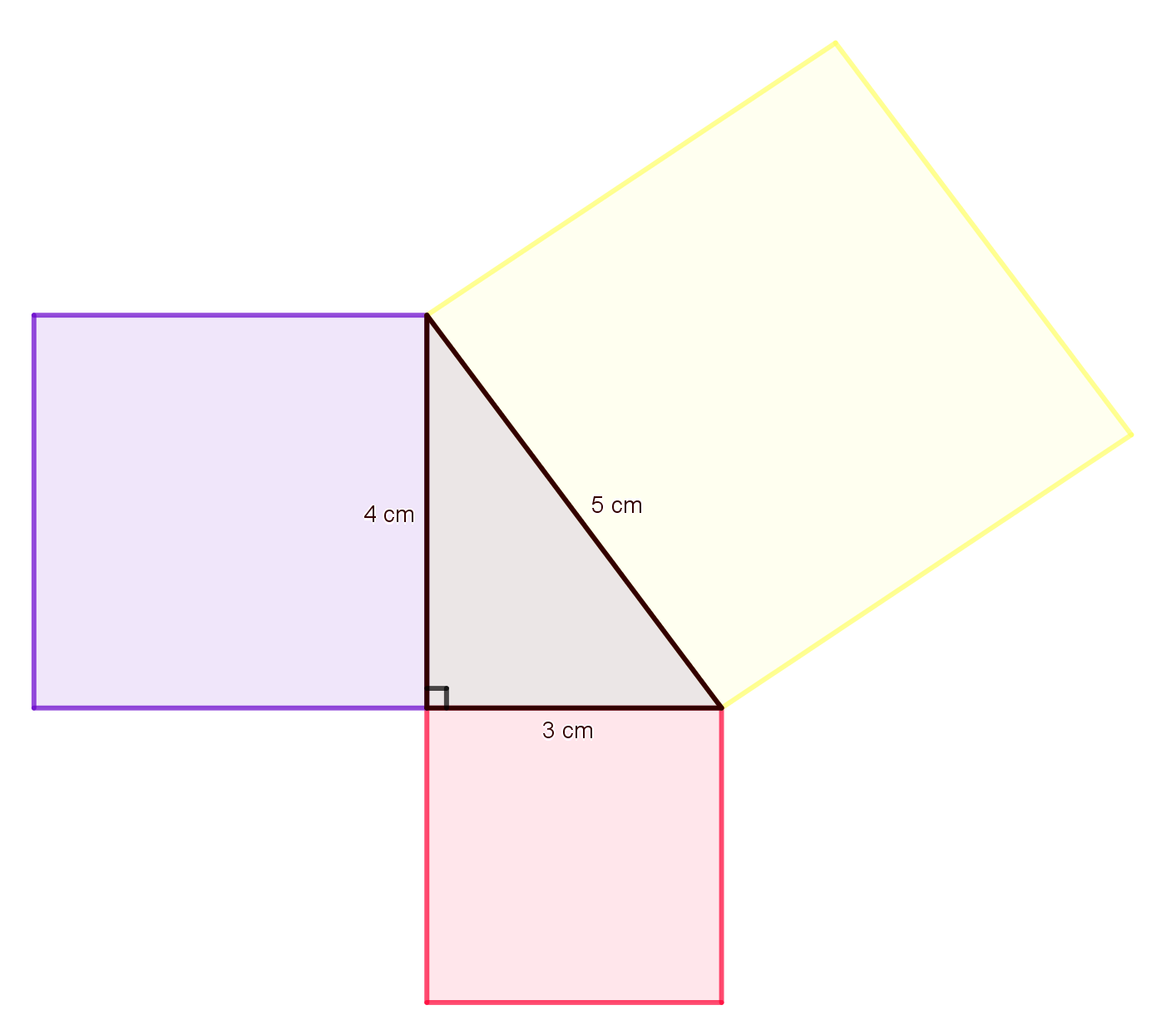
Terminology¶

Hypotenuse: the longest side of a triangle

legs: the other two sides of a triangle that are not the hypotenuse

What is this theorem?¶

When you draw a right angle triangle with a square on each side like this diagram, there’s a relationship between the areas of the squares. You should notice that the areas of the squares on the two legs added together are equal to the area of the largest square on the hypotenuse. In this example, the area of the red square is $9 \text{ cm}^2$, the area of the blue square is $16 \text{ cm}^2$, and the area of the yellow triangle is $25 \text{ cm}^2$.

\[\text{Notice that } \color{red}{9 \text{ cm}^2} + \color{blue}{16 \text{ cm}^2} = \color{yellow}{25 \text{ cm}^2}\]

\[\text{But } \color{red}{3 \text{ cm}} + \color{blue}{4 \text{ cm}} ≠ \color{yellow}{5 \text{ cm}}\]

This relationship actually works for all right angle triangles!

The Pythagorean theorem is $a^2 + b^2 = c^2$ where $a$ and $b$ are the legs and $c$ is the hypotenuse. It does not matter which leg is $a$ or $b$.

Fact: The Pythagorean Theorem is named for the Greek mathematician, Pythagoras.

Pythagorean Triples are sets of three numbers that create a right angle triangle like this one so 3,4,5 is a Pythagorean triple

Example 1¶

Question 1: What are the lengths of the legs of the triangle on the left?¶

The side length of a square is the square root of its area.
The side length of the red square is $\sqrt{4 \text{ m}^2} = 2 \text{ m}$.
The side length of the blue square is $\sqrt{9 \text{ m}^2} = 3 \text{ m}$.
Therefore the lengths of the legs are $2 \text{ m}$ and $3 \text{ m}$.

Question 2: What is the area of the yellow square in the diagram to the left?¶

Let’s use the Pythagorean theorem. The area of the two smaller squares added together is equal to the area of the larger square.
The area of the red square is $ 4 \text{ m}^2$ and the area of the blue square is $ 9 \text{ m}^2$.
Now we add them together: $ 4 \text{ m}^2 + 9 \text{ m}^2 = 13 \text{ m}^2$.
The area of the yellow square is $ 13 \text{ m}^2$.

Question 3: What is the length of the hypotenuse of the triangle to the left?¶

Now we know the area of the large yellow square is $ 13 \text{ m}^2$, so the side length of the square is $\sqrt{13} \text{ m}$.
The hypotenuse of the triangle has the same length as the length of the side of the yellow square.
Therefore the length of the hypotenuse is $\sqrt{13} \text{ m}$.

Proof¶

Not convinced that this relationship works for all right angle triangles? Look at the visual proof from mathisfun.com.

%%html
<iframe width="560" height="315" src="https://www.youtube.com/embed/_87RbSoELW8" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

Algebraic proof¶

We will work through the proof of a² + b² = c² together. Lets look at the diagram below.

You can see the 4 identical right angle triangles within a square, and the sides of each triangle are labelled just like our first example. a = 3, b = 4, and c = 5.

Area of the large square¶

The area of the large square is its side length squared, which is $(3 + 4)^2 = 7^2 = 49.$

Area of the pieces¶

The area of the smaller yellow square in the middle is $ 5^2 = 25.$
The area of one blue triangle is $\frac{3 \times 4}{2}$ and since there’s 4 of them, the area of all 4 triangles is $\frac{4 \times (3 \times 4)}{2} = \frac{4 \times 12}{2} = \frac{48}{2} = 24.$

Now we add those together to ge 25 + 24 = 49.

Areas are equal¶

You can see that $ 49 = 49. $ This is because the area of the large square takes up the exact same space as the ares of all 4 blue triangles and the yellow square.

This doesn’t just work for these numbers though, it works for any numbers that create right angle triangles! If you want to see the full proof without numbers, you can check it out at mathisfun.com.

Example 2¶

Let’s go through an example of a question without the squares. What is the length of the hypotenuse of the triangle below?

Recall the Pythagorean theorem: $a^2 + b^2 = c^2$.
Now let’s put the values we know into the theorem. The length of the hypotenuse is the value of c. $$\begin{align*} (2 \text{ cm})^2 + (5 \text{ cm})^2 & = c^2 \\ 4 \text{ cm}^2 + 25 \text{ cm}^2 & = c^2 \\ 29 \text{ cm}^2 & = c^2 \\ \sqrt{29 \text { cm}^2} & = \sqrt{c^2} \\ \sqrt{29} \text{ cm} & = c \\ \end{align*}$$

Let’s approximate the answer to one decimal place using a calculator. $\sqrt{29} \text{ cm} = 5.4 \text{ cm}$.
The length of the hypotenuse is $\sqrt{29} \text{ cm}$ or approximately $5.4 \text{ cm}$.

Practice¶

Question 1¶

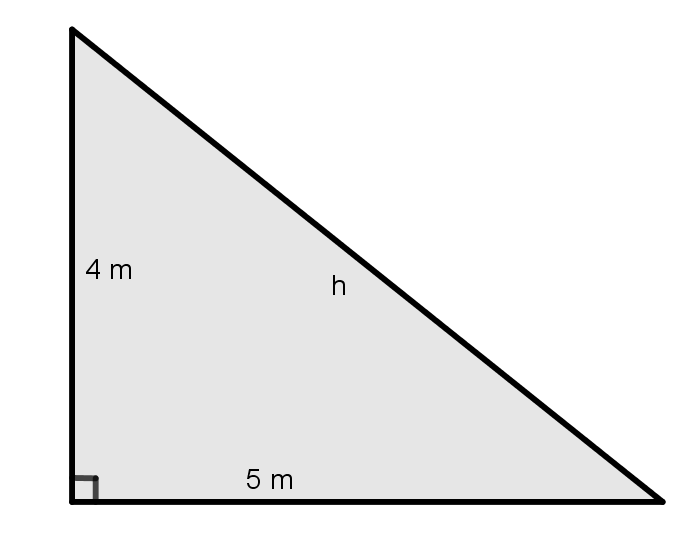
../../../_images/PythagoreanTriangle5.png

answer1 = widgets.RadioButtons(options=['9 m', '6 m','6.4 m','5.4 m'],
                              value=None, description= 'Hypotenuse')

def display1():
    IPython.display.clear_output()
    print("What is the length of the hypotenuse of the triangle above?")
    print("Round to one decimal place when necessary.")
    IPython.display.display(answer1)

def check1(a):
    display1()
    if answer1.value == '6.4 m':
        print("Correct! Great job! The theorem properly filled out looks like this: 16 m² + 25 m² = 41 m²")
    else:
        print("Sorry, that's not right, try again. Pythagorean Theorem is a² + b² = c².")

display1()
answer1.observe(check1, 'value')

What is the length of the hypotenuse of the triangle above?
Round to one decimal place when necessary.

Question 2¶

Let’s have a more practical problem for the Pythagorean theorem. Say you have a table that’s shortest side is 3.10 m long. If the table is held on an angle, can it fit through this door frame below? Round to 2 decimal places.

../../../_images/PythagoreanTriangleDoor.png

answer3 = widgets.RadioButtons(options=['2.00 m', '2.83 m','3.16 m','4.03 m'],
                              value=None, description= 'Diagonal')
    
def display3():
    IPython.display.clear_output()
    print("What is the diagonal of the door?")
    print("Round to two decimal places when necessary.")
    IPython.display.display(answer3)

def check3(a):
    display3()
    if answer3.value == '3.16 m':
        print("Correct! Great job!")
    else:
        print("Sorry, that's not right, try again. Pythagorean Theorem is a² + b² = c².")

display3()
answer3.observe(check3, 'value')

What is the diagonal of the door?
Round to two decimal places when necessary.

answer2 = widgets.RadioButtons(options=['Yes, the table will fit.', 'No, the table will not fit'],
                              value=None)
def display2():
    IPython.display.clear_output()
    print("Is the length of the table smaller than the diagonal of the door?")
    print("Round to two decimal places when necessary.")
    IPython.display.display(answer2) 
    
def check2(a):
    display2()
    if answer2.value == 'Yes, the table will fit.':
        print("That's right! The table will fit through the door on an angle.")
    else:
        print("Sorry, that's not right, the table will be able to fit in the door because 3.1 m is less than 3.16 m.")
            
display2()
answer2.observe(check2, 'value')

Is the length of the table smaller than the diagonal of the door?
Round to two decimal places when necessary.

What else would knowing how to find the hypotenuse be helpful for?

Extend Your Knowledge¶

We can use the Pythagorean theorem for more than just finding the length of the hypotenuse given the two legs. We can find the length of one leg given the other leg and the hypotenuse.

Example¶

Given this right angled triangle below, what is the missing side length?

../../../_images/PythagoreanTriangle6.png

Let’s start by filling in the information we know into the pythagorean theorem. $$\begin{align*} a^2 + b^2 & = c^2 \\ a^2 + (\sqrt{20 \text{ units}})^2 & = (6 \text{ units})^2 \\ \end{align*}$$

Now let’s solve this equation for the missing variable. In this example, we will solve for $a$. $$\begin{align*} a^2 + (\sqrt{20 \text{ units}})^2 & = (6 \text{ units})^2 \\ a^2 + 20 \text{ units}^2 & = 36 \text{ units}^2 \tag{apply the power of 2 to the bases} \\ a^2 + 20 \text{ units}^2 - 20 \text{ units}^2 & = 36 \text{ units}^2 - 20 \text{ units}^2 \tag{subtract 20 units² from both sides} \\ \sqrt{a^2} & = \sqrt{16 \text{ units}^2} \tag{square root both sides} \\ a & = 4 \text{ units} \end{align*}$$

Practice¶

Now you try to calculate the length of the missing leg.

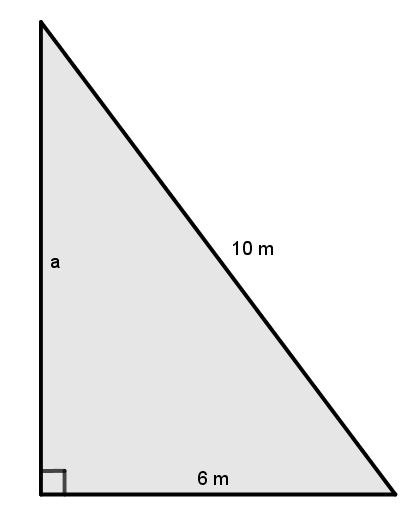
../../../_images/PythagoreanTriangle8.png

answer4 = widgets.RadioButtons(options=['8 m', '9 m','8.3 m','7.8 m'],
                              value=None, description= 'Side Length')

def display4():
    IPython.display.clear_output()
    print("What is the length of the leg labelled a above?")
    print("Round to one decimal place when necessary.")
    IPython.display.display(answer4)

def check4(a):
    display4()
    if answer4.value == '8 m':
        print("Correct! If we divide each side length by 2, you might notice that this triangle is the same one \n as the very first triangle we looked at in this notebook!")
    else:
        print("Sorry, that's not right, try again. Pythagorean Theorem is a² + b² = c². We are looking for a.")

display4()
answer4.observe(check4, 'value')

What is the length of the leg labelled a above?
Round to one decimal place when necessary.

Checking Right angles¶

We can check if a triangle is a right angle triangle by knowing if its sides fit the Pythagorean theorem. If they don’t then it isn’t a right angle triangle. Lets look at an acute and an obtuse triangle and compare their sides in the Pythagorean theorem. You know, just to make sure.

Look at the three triangles below. One is a right angle triangle, one is an acute triangle, and one is an obtuse triangle. Fill in the table below by clicking on the box you want to fill (where it’s written ‘nan’) and typing in your answer. The longest side is side c.

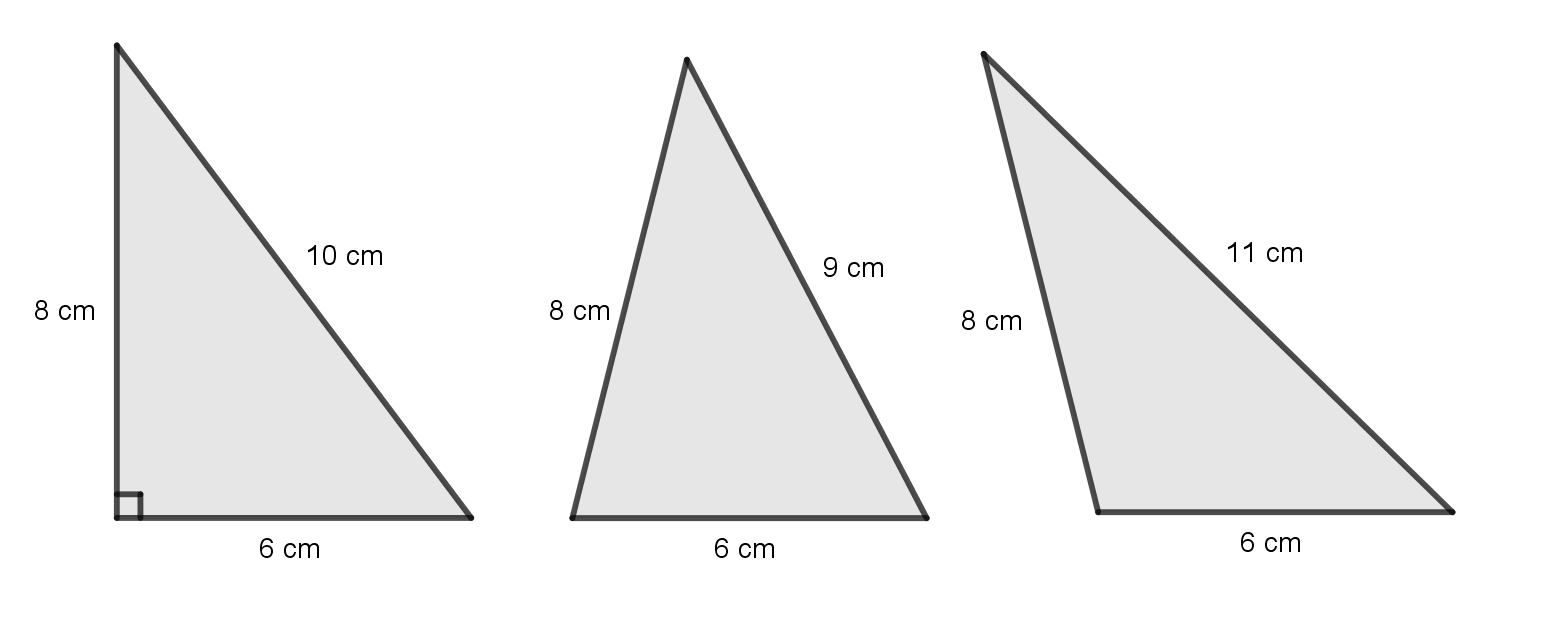
import pandas as pd
import qgrid
table = pd.DataFrame(index=pd.Series(['Right', 'Acute', 'Obtuse']), columns=pd.Series(['a²', 'b²','a² + b²', 'c²']))
table_widget = qgrid.QgridWidget(df =table, show_toolbar=False)
table_widget

answer5 = widgets.RadioButtons(options=['Yes','No'],
                              value=None)

def check5(a):
    IPython.display.clear_output()
    print("Does a² + b² = c² for all triangles?")
    IPython.display.display(answer5)
    if answer5.value == 'No':
        print("That's right! The Pythagorean theorem only works for right angle triangles.")
    else:
        print("Actually, the Pythagorean theorem only works for right angle triangles.")
    print("Now let's use this knowledge to check if triangles have a right angle or not!")

print("Does a² + b² = c² for all triangles?")
IPython.display.display(answer5)
answer5.observe(check5, 'value')

Does a² + b² = c² for all triangles?

Example¶

Let’s go through an example together. Here is a triangle with all three sides labelled. Is this a right angle triangle?

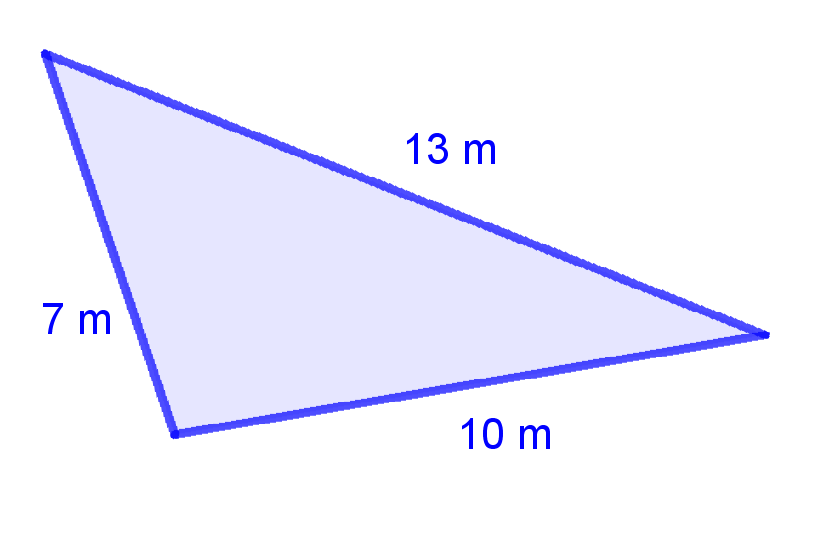
Remember, the longest side is side c. Let’s fill in the Pythagorean theorem and see if the left side equals the right.
Since c is the largest side, a and b will be the legs. $$\begin{align*} \text{Let's start with the left side:} \\ a & = 7 \text{ m} \\ a^2 & = 49 \text{ m}^2 \\ b & = 10 \text{ m} \\ b^2& = 100 \text{ m}^2 \\ \text{Now let's add them together:} \\ a^2 + b^2 & = 49 \text{ m}^2 + 100 \text{ m}^2 \\ a^2 + b^2 & = 149 \text{ m}^2 \\ \end{align*}$$ **The left side equals 149 m²** <br> $$\begin{align*} \text{And now the right side:} \\ c & = 13 \text{ m} \\ c^2 & = 169 \text{ m}^2 \\ \end{align*}$$ The right side equals 169 m²

149 m² does not equal 169 m² therefore this triangle is not a right angle triangle.

Practice¶

Now it’s your turn to check if this triangle below is a right angle triangle.

submit1 = widgets.Button(description='Submit', button_style='success')
answer6 = widgets.Text(value=None, placeholder='Your answer here', description='Left side')

def display6():
    IPython.display.clear_output()
    print("What is a² + b²?")
    print("Type your answer below, and don't forget units! Eg: write 50 cm^2 or 50 units^2")
    IPython.display.display(answer6, submit1)
    submit1.on_click(check6)
    
def check6(a):
    display6()
    if answer6.value == '169 units^2':
        print("That's right! Now let's move on to the right side.")
    else:
        if answer6.value == '169' or answer6.value == '169 units':
            print("Don't forget your units!")
        else:
            print("Sorry, that's not right, try again before moving on to the right side.")
            
display6()

What is a² + b²?
Type your answer below, and don't forget units! Eg: write 50 cm^2 or 50 units^2

submit2 = widgets.Button(description='Submit', button_style='success')
answer7 = widgets.Text(value=None, placeholder='Your answer here', description='Right side')

def display7():
    IPython.display.clear_output()
    print("What is c²?")
    print("Type your answer below, and don't forget units! Eg: write 50 cm^2 or 50 units^2")
    IPython.display.display(answer7, submit2)
    submit2.on_click(check7)
    
def check7(a):
    display7()
    if answer7.value == '169 units^2':
        print("That's correct! Great job!")
    elif answer7.value == '169' or answer7.value == '169 units':
        print("Don't forget your units!")
    else:
        print("Sorry, try again.")
            
display7()

What is c²?
Type your answer below, and don't forget units! Eg: write 50 cm^2 or 50 units^2

answer8 = widgets.RadioButtons(options=['Yes','No'],
                              value=None)

def check8(a):
    IPython.display.clear_output()
    print("Is this triangle a right angle triangle?")
    IPython.display.display(answer8)
    if answer8.value == 'Yes':
        print("That's right! This is a right angle triangle")
    else:
        print("Actually, this triangle is a right angle triangle.")

print("Is this triangle a right angle triangle?")
IPython.display.display(answer8)
answer8.observe(check8, 'value')

Is this triangle a right angle triangle?

Word question¶

frame

Bailey has four pieces of wood. Two of them are 3 inches long. The other two are 5 inches long.
Bailey makes a rectangular picture frame using these pieces. Then the diagonal is measured to be 7 inches long.

answer9 = widgets.RadioButtons(options=['Yes','No'],
                              value=None)

def check9(a):
    IPython.display.clear_output()
    print("Does the picture frame have a right angle corner?")
    IPython.display.display(answer9)
    if answer9.value == 'No':
        print("That's right! The frame does not have a right angle corner.")
    else:
        print("Actually, the frame does not have a right angle corner.")

print("Does the picture frame have a right angle corner?")
IPython.display.display(answer9)
answer9.observe(check9, 'value')

Does the picture frame have a right angle corner?

What did we learn?¶

Lets summarize what we have learned in this notebook:

The Pythagorean theorem states: a² + b² = c²
This theorem has been proven multiple ways
This theorem can be used for multiple purposes
- Find the length of the hypotenuse
- Find the length of a side
- Confirm if there’s a right angle
Lots of situations in life need the Pythagorean theorem

This math concept will be used for many more years in school. Make sure to do lots of practice, even beyond this notebook so that you understand the Pythagorean theorem well.

Callysto Curriculum Notebooks

Pythagorean Theorem¶

Introduction¶

Terminology¶

What is this theorem?¶

Example 1¶

Question 1: What are the lengths of the legs of the triangle on the left?¶

Question 2: What is the area of the yellow square in the diagram to the left?¶

Question 3: What is the length of the hypotenuse of the triangle to the left?¶

Proof¶

Algebraic proof¶

Area of the large square¶

Area of the pieces¶

Areas are equal¶

Example 2¶

Practice¶

Question 1¶

Question 2¶

Extend Your Knowledge¶

Example¶

Practice¶

Checking Right angles¶

Example¶

Practice¶

Word question¶

What did we learn?¶