
Pi Day¶

Some Pi Facts¶
Pi is represented mathematically as the symbol \(\pi\) and is the circumference divided by the diameter of a circle.
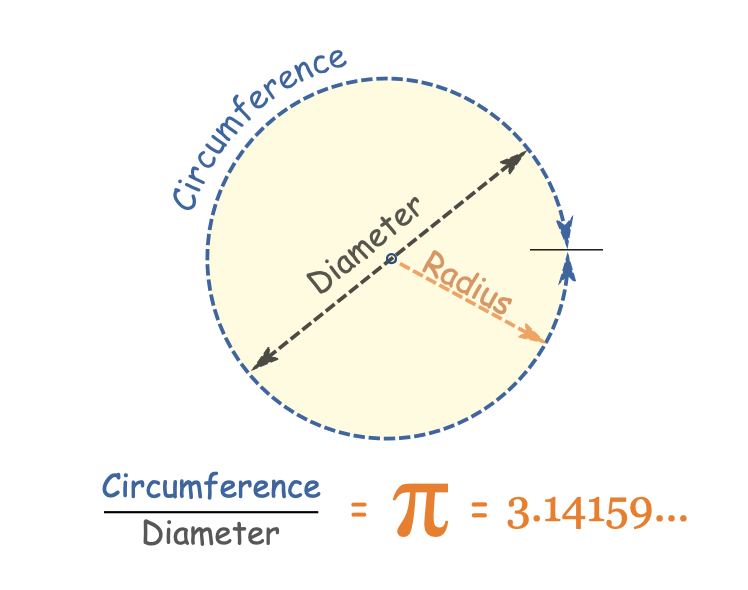
The symbol for Pi (\(\pi\)) was introduced by William Jones in 1706. Before being ascribed a modern name, Pi was known as “quantitas in quam cum multiflicetur diameter, proveniet circumferencia” — Latin for “the quantity which, when the diameter is multiplied by it, yields the circumference.”
Pi is an irrational number - its digits never end or repeat in any known way.
It’s believed that human civilizations were aware of Pi as early as 2550 BC.
Why Do We Celebrate Pi Day?¶

March 14 is Community Pi (π) Day, the annual celebration of a never-ending number—and Albert Einstein’s birthday. How did Pi inspire a national holiday and an international celebration thousands of years after its discovery? It all started at San Francisco’s Exploratorium with former staff physicist, tinkerer, and media specialist Larry Shaw in 1988.
Interactive Pi Fun!¶
Select the code cell below, then click the ▶Run button in the toolbar to run this interactive Pi memory test.
Don’t worry about understanding the code, scroll down to see the resulting interactive game below.
import ipywidgets as widgets
from IPython.display import display, Markdown, Latex, Math, HTML, clear_output, Javascript
digit_answers=[1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3,3,8,3,2,7,9,5,0,2,8,8,4,1,9,7,1]
current_position=0
number_of_mistakes=5
number_of_mistakes_left=number_of_mistakes
digit_widgets=[]
for i in range(len(digit_answers)):
digit_widgets.append(widgets.Text(value='',disabled=True,layout=widgets.Layout(width='3%')))
pi_real=widgets.HTMLMath(value="$$\pi=3.$$")
next_number=widgets.HTML(value="Select the next digit:")
answer_text=widgets.Select(options=['0','1','2','3','4','5','6','7','8','9'],value='0',
description='',disabled=False,layout=widgets.Layout(width='10%'))
warning=widgets.HTML(value="")
mistakes=widgets.HTML(value="Mistakes left: <font color='red'>"+str(number_of_mistakes_left)+"</font>")
reset_button=widgets.Button(description='Reset',disabled=False)
def on_digit_selected(b):
global current_position,number_of_mistakes_left
if answer_text.value == str(digit_answers[current_position]):
digit_widgets[current_position].value=answer_text.value
current_position=current_position+1
warning.value="<font color='green'> Correct! </font>"
else:
warning.value="<font color='red'> Not quite... </font>"
number_of_mistakes_left=number_of_mistakes_left-1
mistakes.value="Mistakes left: <font color='red'>"+str(number_of_mistakes_left)+"</font>"
if number_of_mistakes_left==0 or current_position==len(digit_answers):
b.disabled=True
answer_text.disabled=True
for i in range(len(digit_answers)):
digit_widgets[i].value=str(digit_answers[i])
warning.value="<font color='red'> You scored "+str(current_position)+"! Run the code cell again to start over.</font>"
answer_text.observe(on_digit_selected, names='value')
display(Markdown("**How many digits of $\pi$ can you remember?**"))
display(widgets.HBox([pi_real]+digit_widgets[:17]))
display(widgets.HBox(digit_widgets[17:]))
display(widgets.HBox([next_number,answer_text,warning]))
display(widgets.HBox([mistakes]))
How many digits of $\pi$ can you remember?
According to the Guiness World Records,
the most decimal places of Pi memorised is 70,000! 😍😍😍
This was achieved by Rajveer Meena at VIT University, in Vellore, India, on 21 March 2015. Rajveer wore a blindfold throughout the entire recall, which took nearly 10 hours.

The Pilish Language¶

Pilish is a language in which the lengths of successive words represent the digits of Pi (3.14159265358979…)
One of the earliest example is the following sentence, believed to have been composed by the English physicist Sir James Jeans:
How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics!
The most recent example is the book by Mike Keith “Not A Wake” (Vinculum Press, 2010):
Now I fall, a tired suburbian in liquid under the trees,
Drifting alongside forests simmering red in the twilight over Europe.
▶Run the following code cell to display an interactive Pilish writing checker.
import re
pi_digits=[3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3,3,8,3,2,7,9,5,0,2,8,8,4,1,9,7,1]
text_area1=widgets.Textarea(placeholder='Type something(up to 32 words)',disabled=False,layout=widgets.Layout(height='100px'))
text_area2=widgets.Textarea(disabled=True,layout=widgets.Layout(height='100px'))
submit_button=widgets.Button(description='Submit',button_style='info',disabled=False)
reset_button1=widgets.Button(description='Reset',disabled=False)
warning1=widgets.HTML(value=" ")
def on_button_reset1_clicked(b):
text_area1.value=""
text_area2.value=""
warning1.value=""
reset_button1.on_click(on_button_reset1_clicked)
def on_button_submit_clicked(b):
text=re.sub(r'[^\w\s]',' ',text_area1.value)
text = re.sub("\d+", "", text)
text_list=text.split()
text_len=len(text_list)
if text_len==0:
text_area1.value=""
warning1.value="There is no text, try again!"
else:
if text_len>32:
text_len=32
text_list=text_list[:text_len]
pi_subset=pi_digits[:text_len]
text_list1=[]
word_length=[]
for word in text_list:
lenw=len(word)
word_length.append(lenw)
text_list1.append(word+"("+ str(lenw)+")")
if word_length==pi_subset:
warning1.value=" <font color='green'> Well done! This is written in Pilish!</font>"
else:
warning1.value=" <font color='red'>Not quite. Your sequence is "+' '.join(str(word_length))+", it needs to be "+' '.join(str(pi_subset))+"</font>"
text_area2.value=' '.join(text_list1)
submit_button.on_click(on_button_submit_clicked)
display(Markdown("**Can you write in Pilish?** Remember $\pi=3.1415926535897932384626433832795028841971$..."))
display(Markdown("**Note**: numbers and special characters are excluded."))
vbox1=widgets.VBox([text_area1,widgets.HBox([submit_button,reset_button1])])
vbox2=widgets.VBox([text_area2,warning1])
display(widgets.HBox([vbox1,vbox2]))
Can you write in Pilish? Remember $\pi=3.1415926535897932384626433832795028841971$...
Note: numbers and special characters are excluded.
Calculating Pi with Darts¶
▶Run the following code cell to display a video about this.
%%html
<iframe width="560" height="315" src="https://www.youtube.com/embed/M34TO71SKGk" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
Throwing Darts at a Target (Dart Board) Explainer:
The square that surrounds the dart board has sides of 1 unit in length and the circle (dart board) inside of the square has a diameter of 1 unit.
The number of darts that land in the circle divided by the number of darts in the entire square should be proportional to the area of the circle divided by the area of the square: $\(\frac{n \mspace{3mu} circle}{n \mspace{3mu} square}\propto\frac{A \mspace{3mu} circle}{A \mspace{3mu} square}\)$
The area of the square is 1 (length = 1), and area of the circle is \(\pi\times r^{2}\), where \(r\) (radius) is 0.5: $\(\frac{n \mspace{3mu} circle}{n \mspace{3mu} square}\propto\pi\times r^{2}=\pi\times 0.5^{2}=\frac{\pi}{4}\)$
So we can get Pi by multiplying both parts by 4:
Try it yourself!
▶Run the code cell to plot random darts and calculate an approximation of π. You can change the value of number_of_darts to see what effect that has.
number_of_darts = 1000
import matplotlib.pyplot as plt
%matplotlib inline
import random
circle_centerx=circle_centery=circle_radius=0.5
x_inside=[]
y_inside=[]
x_outside=[]
y_outside=[]
for i in range(number_of_darts):
x=random.random()
y=random.random()
if (x-circle_centerx)**2+(y-circle_centery)**2<circle_radius**2:
x_inside.append(x)
y_inside.append(y)
else:
x_outside.append(x)
y_outside.append(y)
circle2 = plt.Circle((circle_centerx, circle_centery), circle_radius,color='b',fill=False)
fig, ax = plt.subplots(figsize=(10,10))
ax.plot(x_inside,y_inside, 'o', color='y',alpha=0.4)
ax.plot(x_outside,y_outside, 'o', color='r',alpha=0.4)
ax.add_artist(circle2)
plt.ylim(0, 1)
plt.xlim(0, 1)
plt.show()
print("Number of darts inside the circle: "+str(len(x_inside)))
print("Total number of darts: "+str(number_of_darts))
print("Estimated π = ("+str(len(x_inside))+"/"+str(number_of_darts)+")×4 = "+str(len(x_inside)*4/number_of_darts))
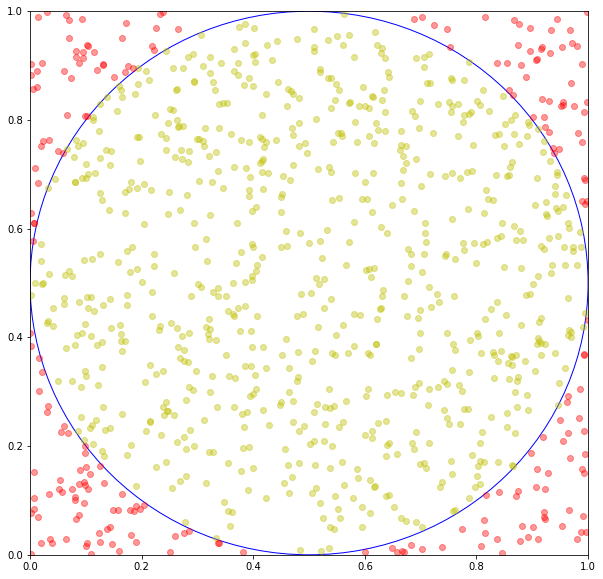
Number of darts inside the circle: 776
Total number of darts: 1000
Estimated π = (776/1000)×4 = 3.104
Calculating Pi ¶
There are exact formulas for calculating Pi but in order to so requires you to do something an infinite number of times.
One of the most well known ways to calculate Pi is to use the Gregory-Leibniz Series:
The problem with this series is that you need to add up a lot of terms in order to get an accurate approximation of Pi. (More than 300 terms need to be added in order to produce Pi accurate to two decimal places!)
Another series which converges more quickly is the Nilakantha Series which was developed around 1500 AD (This means that you need to work out fewer terms for your answer to become closer to Pi):
We can compare these two ways of calculating Pi by plotting each series.
▶Run the code cell to generate the plots.
series_l_x=[0]
series_l_y=[4]
series_n_x=[0]
series_n_y=[3]
ans = 3
j = 2
ans1 = 4
j1 = 3
for step in range(1,50):
series_l_x.append(step)
series_n_x.append(step)
if step % 2 == 1:
ans += 4.0 / (j * (j + 1) * (j + 2))
ans1 -= 4.0 / j1
else:
ans -= 4.0 / (j * (j + 1) * (j + 2))
ans1 += 4.0 / j1
ans=round(ans,15)
ans1=round(ans1,15)
series_n_y.append(ans)
series_l_y.append(ans1)
j += 2
j1 += 2
fig = plt.figure(figsize=(17,7))
plt.scatter(series_n_x,series_n_y)
plt.plot(series_n_x,series_n_y,label='Nilakantha Series')
plt.scatter(series_l_x,series_l_y, color="r")
plt.plot(series_l_x,series_l_y,color="r", label="Gregory-Leibniz Series")
plt.title("Calculating Pi - Infinite Series")
plt.ylabel('Estimated Pi')
plt.xlabel('Number of Elements')
plt.grid()
plt.legend()
plt.show()
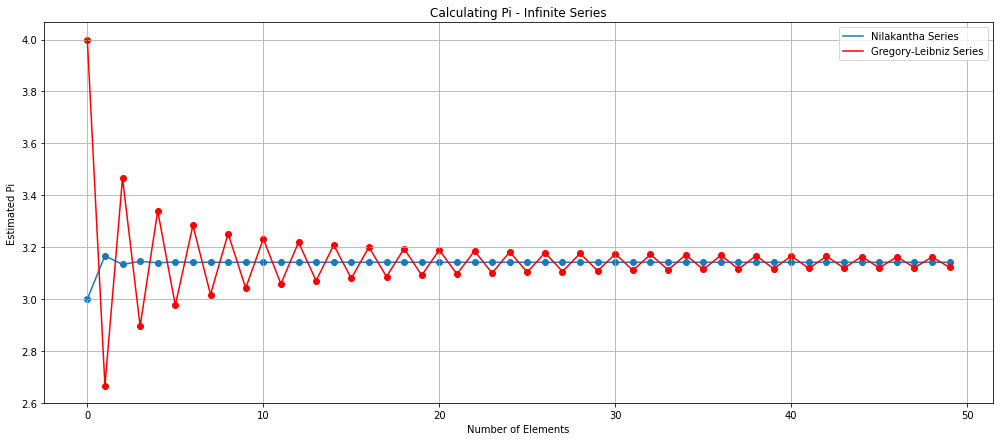
We can see that the Gregory-Leibniz Series shows more variablility than the Nilakantha Series, particularly for smaller numbers of elements. However they do start to converge as the number of elements increases.
History of Calculating Pi ¶
In around 250 BC, Archimedes presented what is thought to be the first rigourous calculation of Pi, using fractions, where \(3.1408 < π < 3.14285\).
In 1600, Ludolph van Ceulen produced a 35 digit approximation of Pi and took 25 years of calculations which were done by hand. Ludolph’s achievement was so great that when he died, his upper and lower bounds for Pi were inscribed on his tombstone.
By 1665, Isaac Newton calculated Pi to 16 decimal places.
It was in the early 1700s that Thomas Lagney calculated 127 decimal places of Pi reaching a new record.
In the second half of the twentieth century, the number of digits of Pi increased from about 2000 to 500,000.
In 2017 a Swiss scientist Peter Trueb computed more than 22 trillion digits of Pi, which stood as the record until…
The record for calculating Pi was set by Emma Haruka Iwao in 2019, who computed Pi to 31,415,926,535,897 digits in 121 days using cloud computing infrastructure!


