Radicans: Simplifying¶

Overview¶

Lesson outcomes¶

Compare and simplify radical expressions with numbers and variables.
Express an entire radical as a mixed radical and vice versa.
Rationalize a radical expression.
Identify values for which the radical expression is defined.

Introduction¶

Radicals (or roots) are the opposite operation of applying exponents: we can undo a power with a radical, and we can undo a radical with a power. For instance, if we square 2, we get 4, and if we “take the square root of 4”, we get 2. In mathematical notation, the previous sentence means the following:

\[2^2 = 4, \quad \text{so} \quad \sqrt{4} = 2\]

The \(\sqrt{}\) symbol used above is called the radical symbol. The expression \(\sqrt{9}\) is read as “root nine”, “radical nine”, or “the square root of nine”.

The figure below should help you understand what we mean by squaring a number

#ggb.file('files/square_numbers.ggb').draw();

%%html
<iframe scrolling="no" title="SquareNumbers" src="https://www.geogebra.org/material/iframe/id/nxyydwdt/width/607/height/403/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="607px" height="403px" style="border:0px;"> </iframe>

Numbers can be raised to powers other than just 2; you can cube things, raise them to the fourth power, raise them to the 100th power, and so forth. In the same way, you can take the cube root of a number, the fourth root, the 100th root, and so forth. To indicate some root other than a square root, you use the same radical symbol, but you insert a number into the radical, tucking it into the check mark. For example:

\[4^3 =64 \qquad \sqrt[3]{64} = 4\]

The \(3\) inside the check mark part is the index of the radical. The \(64\) is the argument of the radical, also called the radicand. Since most radicals you see are square roots, the index is notincluded on square roots.

Throughout this notebook, we will only deal with the square root. The equation for the square root function is

\[y =\sqrt{x}.\]

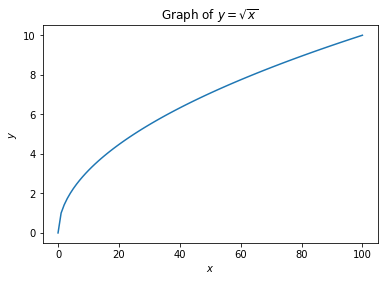
The figure below displays what the graph of the square root looks like.

x = np.linspace(0,100, 100)
y = np.sqrt(x)
plt.plot(x,y)
plt.title("Graph of $y = \sqrt{x}$")
plt.xlabel("$x$")
plt.ylabel("$y$")
axes = plt.gca()
plt.show()

Compare and order radical expressions with numerical radicands.¶

To compare irrational numbers that are square roots, we can simply examine the number that we are taking the square root of. For example, we know that \(\sqrt{15} < \sqrt{17}\) because \(15\) is less than \(17\).

The reason for this is that the function

\[y =\sqrt{x}\]

is increasing. This means that given any two numbers \(a\) and \(b\), if \(a < b\) then \(f(a) < f(b)\), in other words, a function is increasing when the output is always bigger than the input.

Observe the figure below where the points \(5\) and \(10\) are highlighted. Because \(5<10\), then also \(\sqrt{5} <\sqrt{10}\).

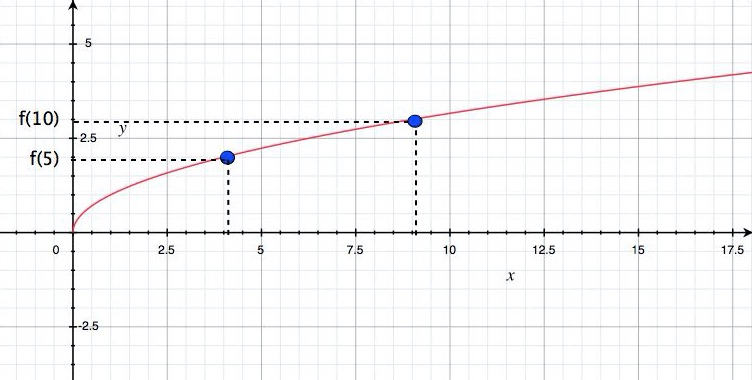
This rule holds for any number under the square root!

Therefore, it is pretty easy to compare and order numerical radicands. You just look at the number under the square root and decide which one is bigger.

Use the activity below to test your understanding.

Is \(\sqrt{45}\) smaller than \(\sqrt{33}\)?

def rad(val):
    if val == "Yes":
        display(Latex("No! $45>33$, therefore $\sqrt{45}>\sqrt{33}$."))
        #display(Latex("This equation has no exponent on either variable, and is therefore linear."))
    elif val == "No":
        display(Latex("Correct!"))

#display(Latex("Is $\sqrt{45}$ smaller than $\sqrt{33}$?"))

    
interact(rad, val = widgets.Dropdown(options=[' ','Yes', 'No'],value = ' ',description = 'Choose One:',disabled = False));

However, if you’re trying to compare a radical expression to a decimal number things may get little bit more tricky.

For example, let’s say you have to decide which number, between \(\sqrt{29}\) and \(5.1\) is bigger.

Well we know that

\[\sqrt{29}>\sqrt{25} = 5,\]

and

\[\sqrt{29}<\sqrt{36} = 6,\]

Because \(29\) is almost halfway between \(25\) and \(36\) we can estimate that \(\sqrt{29}\) would be closer to \(5.5\) than to \(5.1\). Therefore, we can conclude that

\[\sqrt{29} > 5.1.\]

Say now we want to compare \(\sqrt{27}\) and \(5.1\). This time, \(\sqrt{27}\) is much closer to \(\sqrt{25}\) and \(\sqrt{36}\) so it is more complicated to decide which number is bigger.

The safest way to make a decision, in this case, is by squaring \(5.1\) and see if it is bigger that \(27\) or not.

\[5.1^2 = 5.1 \cdot5.1 = 26.01\]

Therefore, \(\sqrt{26.01} = 5.1\). Now, since \(\sqrt{27} > \sqrt{26.01}\), we conclude that

\[\sqrt{27}> 5.1\]

Properties of Radicands¶

Before explaining how to simplify radical expressions, we need to learn about some of their properties.

Product of Radicands

This property lets you take a square root of a product of numbers and break up the radical into the product of separate square roots.

\[\left(\sqrt{ab}\right)^2 = ab = a \cdot b = \left(\sqrt{a}\right)^2 \left(\sqrt{b}\right)^2 = \left(\sqrt{a} \sqrt{b}\right)^2\]

So we have

\[\sqrt{ab} = \sqrt{a}\sqrt{b}\]

Note that this property is valid for all \(a,b \geq 0\)

Another way to think about this property is that the root of the product is the product of the roots.

Quotient of Radicands

This property lets you take a square root of the quotient of numbers and break up the radical into the quotient of separate square roots.

\[\left(\sqrt{\frac{a}{b}}\right)^2 =\frac{a}{b} = \frac{\left(\sqrt{a}\right)^2}{ \left(\sqrt{b}\right)^2 } =\left(\frac{\sqrt{a} }{ \sqrt{b}}\right)^2\]

So we have

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]

This property is valid for all \(a \geq 0\) and for \(b>0\).

Another way to think about this property is that the root of a quotient is the quotient of the roots.

Remark

Also note that while we can break up products and quotients under a radical we can’t do the same thing for sums or differences. In other words,

\[\sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \qquad \sqrt{a - b} \neq \sqrt{a} - \sqrt{b}\]

Simplify square root terms¶

We already learned that taking the quare root of a number is the opposite operation than raising to the power of two. The following table summarizes these results for the first \(10\) positive integers.


\(\sqrt{1}\)	= \(1\)	since	\(1^2\)	= \(1\)
\(\sqrt{4}\)	= \(2\)	since	\(2^2\)	= \(4\)
\(\sqrt{9}\)	= \(3\)	since	\(3^2\)	= \(9\)
\(\sqrt{16}\)	= \(4\)	since	\(4^2\)	= \(16\)
\(\sqrt{25}\)	= \(5\)	since	\(5^2\)	= \(25\)
\(\sqrt{36}\)	= \(6\)	since	\(6^2\)	= \(36\)
\(\sqrt{49}\)	= \(7\)	since	\(7^2\)	= \(49\)
\(\sqrt{64}\)	= \(8\)	since	\(8^2\)	= \(64\)
\(\sqrt{81}\)	= \(9\)	since	\(9^2\)	= \(81\)
\(\sqrt{100}\)	= \(10\)	since	\(10^2\)	= \(100\)

The numbers \(1,4,9,16 \dots\) are called perfect squares and we will use them to simplify square root terms.

To simplify a term containing a square root, we factor out anything that is a perfect square; that is, we factor inside the radical symbol and then we take out in front of that symbol anything that has two copies of the same factor.

This rules still apply when we try to simplify a number under the square root that is not a perfect square.

Consider for instance \(\sqrt{75}\). First of all, we need to factor \(75\) in prime factors.

\[\sqrt{75} = \sqrt{3 \cdot 5 \cdot 5}.\]

Next, we look for any factor that has two copies

\[\sqrt{75} = \sqrt{3 \cdot 5 \cdot 5}= \sqrt{5^2 \cdot 3}.\]

Finally, we take those factors out of the square root symbol using the property for product of radicands that we learned above.

\[\sqrt{75} = \sqrt{3 \cdot 3 \cdot 5}= \sqrt{5^2 \cdot 3} = \sqrt{5^2}\sqrt{3} =5\sqrt{3}.\]

This factorization gives me two copies of the factor \(5\), but only one copy of the factor \(3\). Since I have two copies of \(5\), I can take \(5\) out front. Since I have only the one copy of 3, we have to leave it under the square root.

In this last case, we say that expressed an entire radical with a numerical radicand as a mixed radical.

Consider now \(\sqrt{72}\). It can be decomposed as

\[\sqrt{72} = \sqrt{3 \cdot 3 \cdot 2 \cdot 2 \cdot 2} = \sqrt{3^2 \cdot 2^2 \cdot 2}\]

Because the last \(2\) under the square root does not come as a pair of factor, we have to leave it under the square root.

Therefore we have

\[\sqrt{72} = \sqrt{3 \cdot 3 \cdot 2 \cdot 2 \cdot 2} = \sqrt{3^2 \cdot 2^2 \cdot 2} = 3\cdot 2\sqrt{2} = 6\sqrt{2}.\]

As another example consider \(\sqrt{720}\)

\[\sqrt{720}= \sqrt{3 \cdot 3 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} = \sqrt{3^2 \cdot 2^2 \cdot 2^2 \cdot 5} = 3\cdot2\cdot2\sqrt{5} = 12 \sqrt{5}.\]

Use the following activity to test your understanding.

%%html
<iframe scrolling="no" title="MixedRadicals" src="https://www.geogebra.org/material/iframe/id/g3gyde4q/width/801/height/411/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="801px" height="411px" style="border:0px;"> </iframe>

Express a mixed radical with a numerical radicand as an entire radical¶

In the next section, we will learn how to express a mixed radical as an entire radical.

Keeping in mind that any number can be written as the square root of its square, you can use this strategy to write a mixed radical as an entire radical by writing the leading number as a radical, then multiplying the radicands.

Example 1

Express \(3\sqrt{2}\) as an entire radical.

We know that the index of \(3\sqrt{2}\) is \(2\) so we can write

\[3\sqrt{2} = \sqrt{3^2}\sqrt{2} = \sqrt{9}\sqrt{2} = \sqrt{9\cdot 2}=\sqrt{18}.\]

Example 2

Express \(5\sqrt{7}\) as an entire radical.

We know that the index of \(5\sqrt{7}\) is again \(2\) so we can write

\[5\sqrt{7} = \sqrt{5^2}\sqrt{7} = \sqrt{25}\sqrt{7} = \sqrt{25\cdot 7} = \sqrt{175}.\]

Test you knowledge with the following activities.

Is \(2\sqrt{4}\) greater than \(4\sqrt{2}\)?

def rad(val):
    if val == "Yes":
         display(Latex("Try again!"))
    elif val == "No":
        display(Latex("Correct!"))       
        display(Latex("$4\sqrt{2} = \sqrt{4^2}\sqrt{2} = \sqrt{16}\sqrt{2} = \sqrt{32}.$"))
        display(Latex("$2\sqrt{4} = \sqrt{2^2}\sqrt{4} = \sqrt{4}\sqrt{4} = \sqrt{16}.$"))

#display(Latex("Is $2\sqrt{4}$ greater than $4\sqrt{2}$?"))

    
interact(rad, val = widgets.Dropdown(options=[ ' ', 'Yes', 'No'],value = ' ',description = 'Choose One:',disabled = False));

Express \(6\sqrt{2}\) as an entire radical

#display(Latex("Express $6\sqrt{2}$ as an entire radical"))
#display(Latex("Write your answer as sqrt(your answer)"))



attempts_1 = 0
exercise_1 = w.Text( placeholder='Your answer', description='$\sqrt{}$', disabled=False )
display(exercise_1)

button_exercise_1 = w.Button(button_style='info',description="Enter", layout=Layout(width='15%', height='30px') )
button_exercise_1.on_click(rerun_cell)
display(button_exercise_1)

# Exercise 1 user answer handling

user_answer = exercise_1.value
expected_answer =  '72'

if attempts_1 == 0:
    attempts_1 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_1 >= 4):
        
        exercise_1.disabled = True
        button_exercise_1.disabled = True
        
        display(Markdown("#### The aswer is $6\sqrt{2} = \sqrt{36}\sqrt{2} = \sqrt{72}$"))

    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_1.disabled = True
        button_exercise_1.disabled = True
        
    else:
        
        attempts_1 += 1
        
        if(attempts_1 <= 4):
            display(Markdown("# Please try again."))

Perform one or more operations to simplify radical expressions with numerical or variable radicands¶

When square roots include variables, they are still simplified the same way. We just have to work with variables as well as numbers.

We follow again these basic steps:

Factor the radicand (the numbers/variables inside the square root). Factor the number into its prime factors and expand the variable(s).
Bring any factor listed twice in the radicand to the outside.

Consider for example

\[\sqrt{9x^2y} = \sqrt{(3 \cdot 3)\cdot (x \cdot x) \cdot y} = \sqrt{3^2 \cdot x^2 \cdot y} = \sqrt{3^2}\sqrt{x^2}\sqrt{y} = 3x\sqrt{y}.\]

Since there was a pair of \(3\)’s and a pair of \(x\)’s, we brought the \(3\) and the \(x\) outside, but the \(y\) stayed inside since it was not a pair.

As another example consider \(\sqrt{7a^5}\)

\[\sqrt{7a^5} = \sqrt{7\cdot ({a}\cdot a)\cdot (a\cdot a) \cdot a} = \sqrt{7 \cdot a^2 \cdot a^2 \cdot a} = \sqrt{7} \cdot \sqrt{a^2} \cdot \sqrt{a^2} \cdot \sqrt{a} = a \cdot a \sqrt{7}\sqrt{a} = a^2\sqrt{7a}.\]

Notice that there were two pairs of \(a\)’s, so we were able to bring two to the outside. The last \(a\), however, was not part of a pair and thus stayed inside.

Test you understanding with the following activity.

Express \(\sqrt{12a^2c}\) as a mixed radicand.

#display(Latex("Express $\sqrt{12a^2c}$ as a mixed radicand"))
#display(Latex("Write your answer as (factors outside of the square root)sqrt(factors inside of the square root) "))


attempts_2 = 0
exercise_2 = w.Text( placeholder='Factors outside the square root', description='', disabled=False ) 
display(exercise_2)

button_exercise_2 = w.Button(button_style='info',description="Enter", layout=Layout(width='10%', height='30px') )
button_exercise_2.on_click(rerun_cell)
display(button_exercise_2)

# Exercise 2 user answer handling

user_answer = exercise_2.value
expected_answer =  '2a'

if attempts_2 == 0:
    attempts_2 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_2 >= 4):
        
        exercise_2.disabled = True
        button_exercise_2.disabled = True
        
        display(Latex("The answer is $2a$ because $\sqrt{12a^2c}$ factors as  $\sqrt{2\cdot2\cdot 3\cdot a \cdot a \cdot c}$"))

    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_2.disabled = True
        button_exercise_2.disabled = True
        
    else:
        
        attempts_2 += 1
        
        if(attempts_2 <= 4):
            display(Markdown("# Please try again."))

attempts_3 = 0

exercise_3 = w.Text( placeholder='Factors inside the square root', description='$\sqrt{}$', disabled=False )
display(exercise_3)

button_exercise_3 = w.Button(button_style='info',description="Enter", layout=Layout(width='10%', height='30px') )
button_exercise_3.on_click(rerun_cell)
display(button_exercise_3)

# Exercise 3 user answer handling

user_answer = exercise_3.value
expected_answer =  '3c'

if attempts_3 == 0:
    attempts_3 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_3 >= 4):
        
        exercise_3.disabled = True
        button_exercise_3.disabled = True
        
        display(Latex("The answer is $2a$ because $\sqrt{12a^2c}$ factors as  $\sqrt{2\cdot2\cdot 3\cdot a \cdot a \cdot c}$"))

    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_3.disabled = True
        button_exercise_3.disabled = True
        
    else:

        attempts_3 += 1
        
        if(attempts_3 <= 4):
            display(Markdown("# Please try again."))

Rationalize the monomial denominator of a radical expression¶

The result of taking the square root of a number that is not a perfect square, for example \(\sqrt{5}\), is an irrational number. In the case we are working with fraction, if the irrational number appears in the denominator, we usually want to rationalize it by getting rid of all radicals that are in the denominator.

For example, assume we want to rationalize the following fraction

\[\frac{4}{\sqrt{6}}\]

Step 1 Multiply numerator and denominator by a radical that will get rid of the radical in the denominator.

Since we have a square root in the denominator, then we need to multiply by the square root of an expression that will give us a perfect square under the radical in the denominator.

\[\frac{4}{\sqrt{6}}\cdot \frac{\sqrt{6}}{\sqrt{6}} = \frac{4\sqrt{6}}{\sqrt{36}}\]

Notice that the denominator now has a perfect square under the square root.

Step 2 Simplify the radicals.

Here we notice that the square root of \(36\) is \(6\)

\[\frac{4\sqrt{6}}{\sqrt{36}} = \frac{4\sqrt{6}}{6}\]

Step 3 Simplify the fraction.

Divide numerator and denominator by the common factor of \(2\).

\[ \frac{4\sqrt{6}}{6} = \frac{2\sqrt{6}}{3}\]

An another example consider

\[\frac{32}{\sqrt{8}}\]

Step 1

First of all, we want to multiply by the square root of an expression that will give us a perfect square under the radical in the denominator.

\[\frac{32}{\sqrt{8}}\cdot \frac{\sqrt{8}}{\sqrt{8}} = \frac{32\sqrt{8}}{\sqrt{64}}\]

Step 2

Next, we notice that the square root of \(64\) is \(8\)

\[\frac{32\sqrt{8}}{\sqrt{64}} = \frac{32\sqrt{8}}{8}\]

Step 3

Finally, we simplify the fraction

\[ \frac{32\sqrt{8}}{8} = 4\sqrt{8}.\]

The reason why we choose to rationalize a radical expression is because they are easier to understand. For example, consider \(\frac{7}{\sqrt{8}}\). We learned that

\[\frac{7}{\sqrt{8}} = \frac{7\sqrt{8}}{8}.\]

If you think about it, it is easier to divide a number by a whole number: dividing \(7\sqrt{8}\) by \(8\) is simpler that dividing \(7\) by \(\sqrt{8}\)!

However, it is very important that you remember that the value of radical expression before and after rationalizing does not change!

Test your understanding using the activity below.

Rationalize and simplify \(\frac{13}{\sqrt{7}}\).

#display(Latex("Rationalize and simplify $\\frac{13}{\sqrt{7}}$"))
#display(Latex("Write your answer as (factor)sqrt(factor)/factor "))


attempts_4 = 0
exercise_4 = w.Text( placeholder='Factors at the nominator outside the square root', description='', disabled=False )
display(exercise_4)

button_exercise_4 = w.Button(button_style='info',description="Enter", layout=Layout(width='20%', height='30px') )
button_exercise_4.on_click(rerun_cell)
display(button_exercise_4)

# Exercise 1 user answer handling

user_answer = exercise_4.value
expected_answer =  '13'

if attempts_4 == 0:
    attempts_4 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_4 >= 4):
        
        exercise_4.disabled = True
        button_exercise_4.disabled = True
        
    
        display(Markdown("#### The aswer is $13$"))

        
    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_4.disabled = True
        button_exercise_4.disabled = True
        
    else:
        
        attempts_4 += 1
        
        if(attempts_4 <= 4):
            display(Markdown("# Please try again."))

attempts_5 = 0
exercise_5 = w.Text( placeholder='Factors at the nominator inside the square root', description='$\sqrt{}$', disabled=False )
display(exercise_5)

button_exercise_5 = w.Button(button_style='info',description="Enter", layout=Layout(width='20%', height='30px') )
button_exercise_5.on_click(rerun_cell)
display(button_exercise_5)

# Exercise 1 user answer handling

user_answer = exercise_5.value
expected_answer =  '7'

if attempts_5 == 0:
    attempts_5 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_5 >= 4):
        
        exercise_5.disabled = True
        button_exercise_5.disabled = True
        
    
        display(Markdown("#### The aswer is $7$"))

        
    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_5.disabled = True
        button_exercise_5.disabled = True
        
    else:
        
        attempts_5 += 1
        
        if(attempts_5 <= 4):
            display(Markdown("# Please try again."))

attempts_6 = 0
exercise_6 = w.Text( placeholder='Denominator', description='', disabled=False )
display(exercise_6)

button_exercise_6 = w.Button(button_style='info',description="Enter", layout=Layout(width='15%', height='30px') )
button_exercise_6.on_click(rerun_cell)
display(button_exercise_6)

# Exercise 6 user answer handling

user_answer = exercise_6.value
expected_answer =  '7'

if attempts_6 == 0:
    attempts_6 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_6 >= 4):
        
        exercise_6.disabled = True
        button_exercise_6.disabled = True
        
    
        display(Markdown("#### The aswer is $7$"))

        
    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct."))
        
        exercise_6.disabled = True
        button_exercise_6.disabled = True
        
    else:
        
        attempts_6 += 1
        
        if(attempts_6 <= 4):
            display(Markdown("# Please try again."))

Identify values of the variable for which the radical expression is defined¶

We cannot have a negative inside number a square root. This can be better understood by looking at the graph of the square root we’ve seen at the beginning of this notebook.

You see that the function only branches from the origin to the positive side of the \(x\) axis. This means that the square root is not defined (in other words, ‘cannot handle’) values of \(x\) that are negative.

In particular, consider taking the square root of \(-4\). You quickly realize that this is not possible as there is no real number that squares to \(-4\).

\[\sqrt{-4} \neq -2, \]

as we can verify by squaring

\[(-2)^2 = + 4 \neq -4.\]

We must have a positive value inside the square root. This fact can be important for defining and graphing functions.

The exception is for imaginary (also called complex) numbers.

Another way to see why the square root cannot take negative values is to consider a square with side length \(l\). We know that the area \(A\) of the square is given by

\[A = l \times l= l^2.\]

Therefore

\[l = \sqrt{A}.\]

%%html
<iframe scrolling="no" title="SquareArea" src="https://www.geogebra.org/material/iframe/id/bcukxbwx/width/611/height/470/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="611px" height="470px" style="border:0px;"> </iframe>

Because the area of a square (or of any geometric figure!) cannot be negative, we cannot compute the square root of negative number.

In the following exercise you will learn about what happens to the number zero.

What is \(\sqrt{0}\)?

Hint. Think about it..what do you get if you multiply any number by \(0?\)

#display(Latex("What is $\sqrt{0}?$"))
#display(Latex("Write your answer as sqrt(your answer)"))


#display(Latex("Hint. Think about it..what do you get if you multiply any number by $0?$"))


attempts_7 = 0
exercise_7 = w.Text( placeholder='Your answer', description='$\sqrt{}$', disabled=False )
display(exercise_7)

button_exercise_7 = w.Button(button_style='info',description="Enter", layout=Layout(width='15%', height='30px') )
button_exercise_7.on_click(rerun_cell)
display(button_exercise_7)

# Exercise 7 user answer handling

user_answer = exercise_7.value
expected_answer =  '0'

if attempts_7 == 0:
    attempts_7 += 1
else:
    # Close the option to keep attempting the answer 
    if(attempts_7 >= 4):
        
        exercise_7.disabled = True
        button_exercise_7.disabled = True
        
    
        display(Markdown("#### The aswer is $0$ because $0 \cdot 0 = 0^2 =  0$."))

        
    # If answer is correct, display appropriate markdown cells
    
    if(user_answer == expected_answer):
        
        display(Markdown("#### Your answer is correct! The square root of $0$ is $0$ because $0 \cdot 0 = 0^2 =  0$."))
        
        exercise_7.disabled = True
        button_exercise_7.disabled = True
        
    else:
        
        attempts_7 += 1
        
        if(attempts_7 <= 4):
            display(Markdown("# Please try again."))

Conclusion¶

In this notebook we learnt

The square root is an increasing function, therefore comparing radicals under the square root is easy.
The value of a fraction doesn't change before and after we rationalized it.
We can only take the square root of any number greater than or equal than zero.

Callysto Curriculum Notebooks