Triangles: Area¶

Grade 7 Curriculum¶

This is a notebook on how to calculate the area of a triangle. In this notebook, we will focus on how to calculate the area of any triangle. We will also learn how to find out the length of one variable, either base or height, while given the other variable and the area.

This notebook will help you understand how to find the area of a triangle, and give a few practice questions. This one notebook won’t be enough practice to master this skill, so be sure to do lots of practice!

What is a triangle?¶

A triangle is defined as a 2D shape with 3 straight sides and 3 angles, which can take many forms:

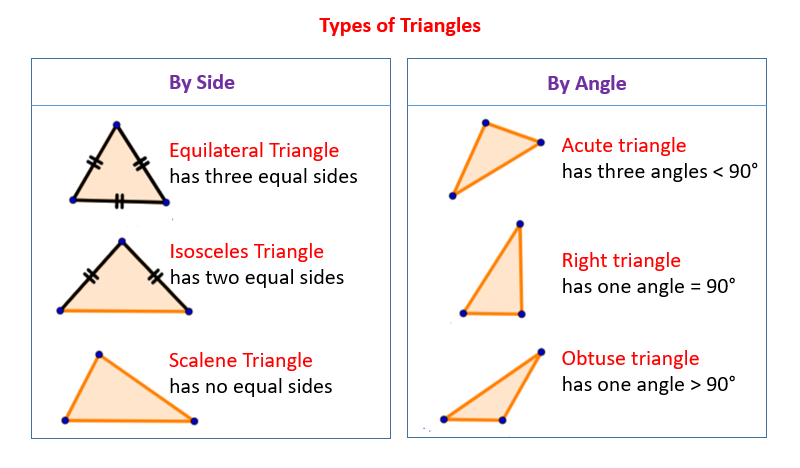www.onlinemathlearning.com

How to find the area¶

Finding the area of a triangle seems a little trickier than finding the area of a rectangle, but there’s an easy way to look at it.

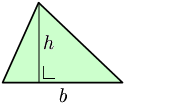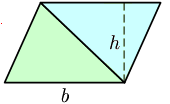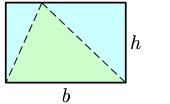
In the picture below, a right angle triangle is created by cutting a rectangle diagonally in half. This makes two triangles with equal areas. We can see that the area of one triangle is half of the area of the rectangle. Since the area of a rectangle is \(\text{base} \times \text{height}\), the area of a triangle would be \(\frac{\text{base } \times \text{ height}}{2}\). Sometimes it’s written as \(\frac{1}{2} \times \text{base} \times \text{height}\), though they both mean the same thing. We will use the first formula to keep it simple.

www.homeschoolmath.net

What about non-right angle triangles?¶

If non-right angle triangles aren’t created out of rectangles, then how can we calculate their area?

Non-right angled triangles aren’t created out of cutting a rectangle, but we get another shape when they’re doubled: a parallelogram! We know from the Area of a Parallelogram notebook that a parallelogram has the same area formula as a rectangle. Now we can figure out the area of any triangle like this:

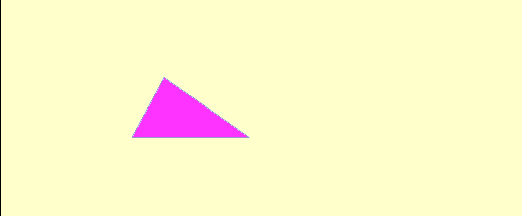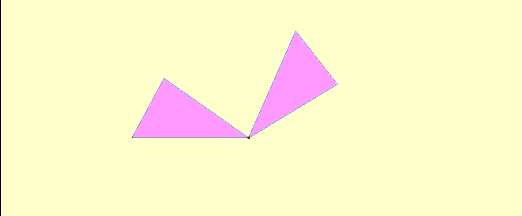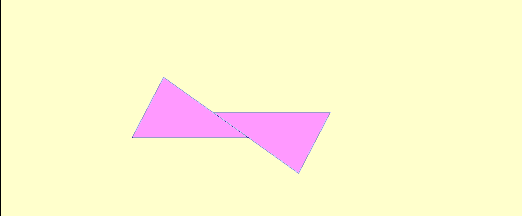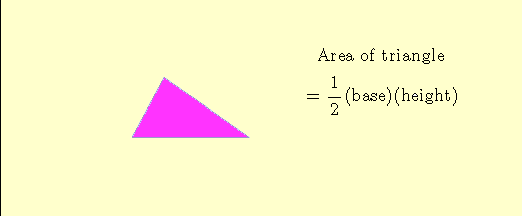animation with words http://people.wku.edu/tom.richmond/triangle1.html

We can also create rectangles out of non-right angle triangles by moving the area around, like this:

animation www.wikimedia.org

Or if you only work with the original area, we can create a rectangle like this:

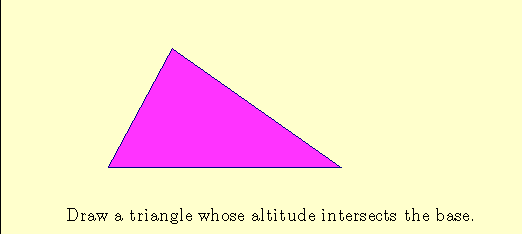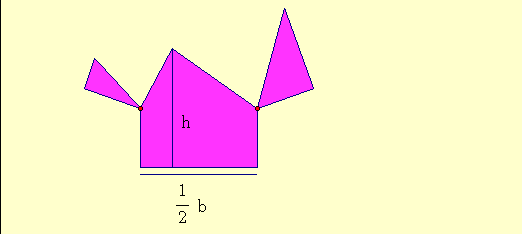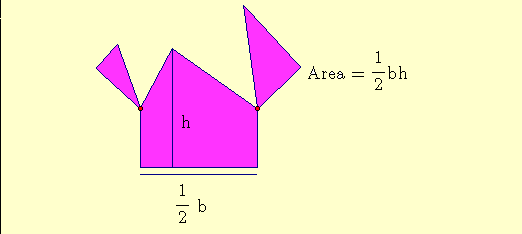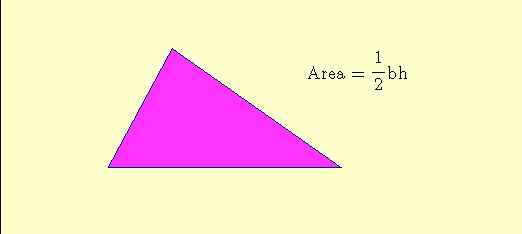animation3 http://people.wku.edu/tom.richmond/triangle2.html

Formula¶

So we can see that no matter what kind of triangle you’re faced with, as long as we know the base and the height, the area of the triangle will be

\[\frac{\text{base } \times \text{ height}}{2}\]

We are going to write base as b and height as h in the practice questions.

Still not convinced?¶

Choose a length for the base and height then slide point \(P\) back and forth on the triangle below and watch the area to see if it changes based on the triangle you make. Try making an obtuse triangle, a right-angle triangle, and an acute triangle.

%%html
<iframe scrolling="no" title="TriangleAnimation1" src="https://www.geogebra.org/material/iframe/id/QgWDn3pt/width/800/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="800px" height="500px" style="border:0px;"> </iframe>

Let’s try it with some numbers¶

Let’s look at this triangle:

Image('images/TriStep1.png',width=300,height=400)

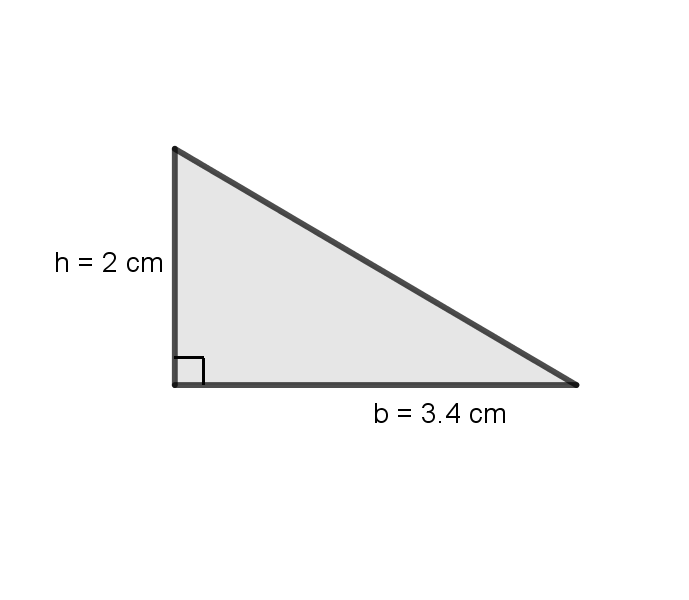
We can see that the height is 2 cm and the base is 3.4 cm. Let’s duplicate this triangle and create a rectangle out of both triangles:

Image('images/TriStep2.png',width=300,height=400)

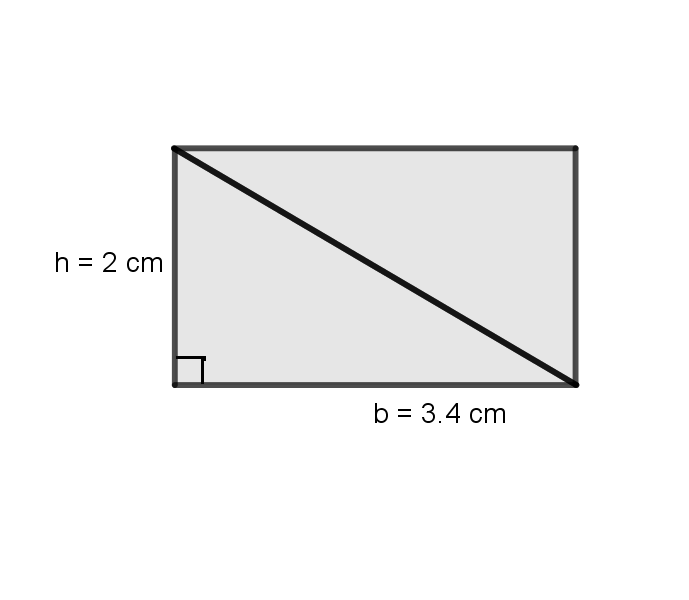
Now we have a rectangle, which we know how to calculate the area for using the formula

\[\begin{split}\begin{align*} \text{Area of rectangle} & = \text{base} \times \text{height}\\ \text{Area of rectangle} & = 2 \text{ cm} \times 3.4 \text{ cm}\\ \text{Area of rectangle} & = 6.8 \text{ cm}^2 \end{align*}\end{split}\]

Since the triangle makes up only half of this rectangle, we have to divide the area in half as well.

\[\begin{split}\begin{align*} \text{Area of triangle} & = \text{Area of rectangle} \div 2\\ \text{Area of triangle} & = 6.8 \text{ cm}^2 \div 2\\ \text{Area of triangle} & = 3.4 \text{ cm}^2 \end{align*}\end{split}\]

Therefore the area of the triangle by itself is \(3.4 \text{ cm}^2\)

Now let’s use our formula!¶

\[\begin{split} \begin{align*} \text{Area of triangle} & = \frac{\text{base} \times \text{height}}{2}\\ \text{Area of triangle} & = \frac{3.4 \text{ cm} \times 2 \text{ cm}}{2}\\ \text{Area of triangle} & = \frac{6.8 \text{ cm}^2}{2}\\ \text{Area of triangle} & = 3.4 \text{ cm}^2 \end{align*}\end{split}\]

As you can see, we get the same answer!

Question 1¶

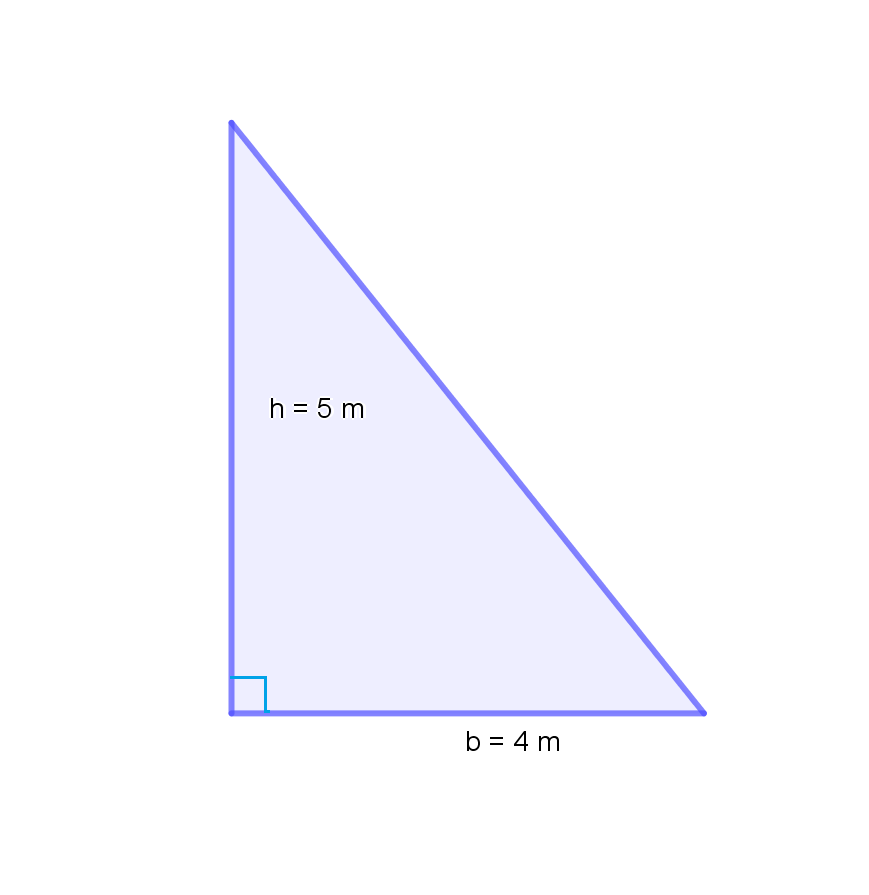
Image('images/TriQ1.png',width=300,height=400)

ans = widgets.Text(value='',placeholder='0',description='Area=',continuous_update=False)

def display():
    print("What is the area of this triangle?")
    IPython.display.display(ans)

def check(a):
    IPython.display.clear_output(wait=True)
    display()
    if ans.value == '10m^2' or ans.value == '10 m^2':
        print("Great job!")
    else:
        if ans.value == '':
            pass
        if ans.value == '10':
            print("Don't forget units! Remember that area is given in square units.")
            print("You can include units in your answer by typing cm^2, m^2, or mm^2.")
        else:
            print("Not quite, don't forget the formula.")

display()
ans.observe(check, 'value')

What is the area of this triangle?

Question 2¶

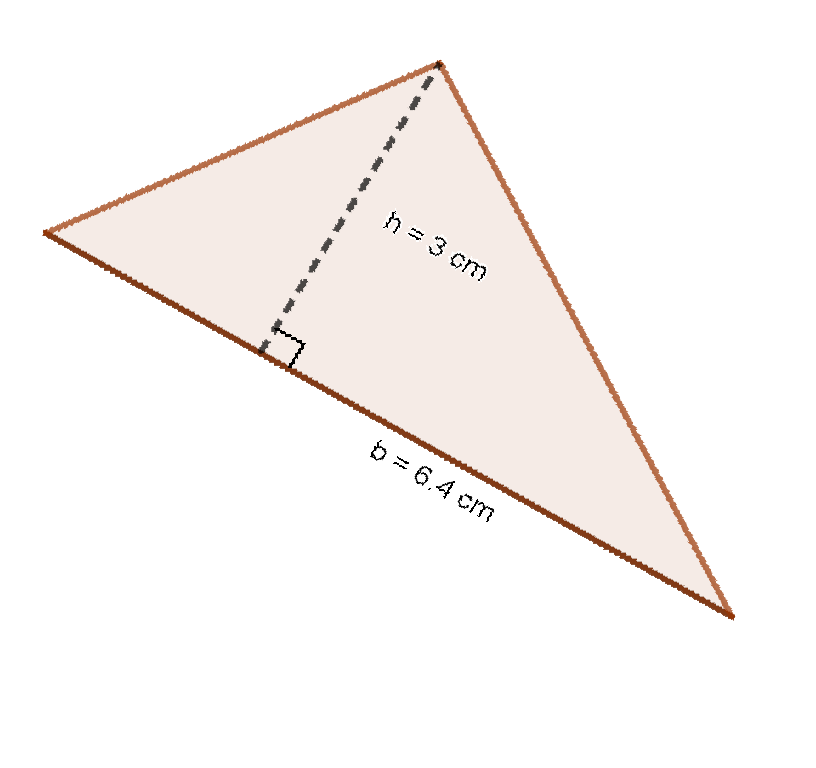
Image('images/TriQ2.png',width=300,height=400)

ans2 = widgets.Text(value='',placeholder='0',description='Area=',continuous_update=False)

def display2():
    print("What is the area of this triangle?")
    IPython.display.display(ans2)

def check2(a):
    IPython.display.clear_output(wait=True)
    display2()
    if ans2.value == '9.6 cm^2' or ans2.value == '9.6cm^2':
        print("Great job!")
    else:
        if ans2.value == '':
            pass
        if ans2.value == '9.6':
            print("Don't forget units! Remember that area is given in square units.")
            print("You can include units in your answer by typing cm^2, m^2, or mm^2.")
        else:
            print("Not quite, don't forget the formula.")

display2()
ans2.observe(check2, 'value')

What is the area of this triangle?

Image('images/TriQ3.png',width=400,height=500)

ans3 = widgets.Text(value='',placeholder='0',description='Area=',continuous_update=False)

def display3():
    print("What is the area of this triangle?")
    IPython.display.display(ans3)

def check3(a):
    IPython.display.clear_output(wait=True)
    display3()
    if ans3.value == '7.52m^2' or ans3.value == '7.52 m^2':
        print("Great job!")
    else:
        if ans3.value == '':
            pass
        if ans3.value == '7.52' or ans3.value == '7.52m' or ans3.value == "7.52 m":
            print("Don't forget units! Remember that area is given in square units.")
            print("You can include units in your answer by typing cm^2, m^2, or mm^2.")
        else:
            print("Not quite, don't forget the formula.")

display3()
ans3.observe(check3, 'value')

What is the area of this triangle?

How does a change in height affect the area?¶

Let’s take the first triangle from the example we went through where the base is 3.4 cm and the height is 2 cm which we figured out the area is \(3.4\text{ cm}^2\). What do you think would happen to the area if we doubled the height to 4 cm? Let’s calculate it:

\[\begin{split} \begin{align*} \text{Area of triangle} & = \frac{\text{base} \times \text{height}}{2}\\ \text{Area of Triangle} & = \frac{3.4 \text{ cm} \times 4 \text{ cm}}{2}\\ \text{Area of Triangle} & = \frac{13.6\text{ cm}^2}{2}\\ \text{Area of Triangle} & = 6.8 \text{ cm}^2 \end{align*} \end{split}\]

Interesting. The new area, \(6.8 \text{ cm}^2\) is double the amount of the old area, \(3.4 \text{ cm}^2\). Perhaps that was just a coincidence? There’s a slider over the next triangle labelled height, slide it to double the current height and look at what happens to the area. Can we generalize that when the height is doubled then the area is doubled?

How does a change in base affect the area?¶

Now instead of changing the height, let’s double the base of the triangle in the first example to 6.8 cm and keep the height at 2 cm. How will this new area compare to the old area? How will it compare to the area when we changed the height? Let’s calculate it:

\[\begin{split} \begin{align*} \text{Area of triangle} & = \frac{\text{base} \times \text{height}}{2}\\ \text{Area of triangle} & = \frac{6.8 \text{ cm} \times 2 \text{ cm}}{2}\\ \text{Area of triangle} & = \frac{13.6 \text{ cm}^2}{2}\\ \text{Area of triangle} & = 6.8 \text{ cm}^2 \end{align*} \end{split}\]

Look at that! This new area is the same as when we doubled the height! Let’s confirm that doubling the base doubles the area by using the slider labelled base over the triangle below to double the base length and watch what happens to the area.

Note: you can slide P back and forth to create right-angle, obtuse, and acute triangles!

%%html
<iframe scrolling="no" title="TriangleAnimation2" src="https://www.geogebra.org/material/iframe/id/QgWDn3pt/width/800/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="800px" height="500px" style="border:0px;"> </iframe>

What conclusion can we draw?¶

By trying different values for base and height of the triangle above, we can safely conclude that doubling the base or doubling the height will double the area.

Let’s extend this conclusion:

What would happen to the area if the base or the height were halved?

Go back to the triangle above and try it!

Practice¶

Lets use what you’ve learned to answer these questions:

Question 1¶

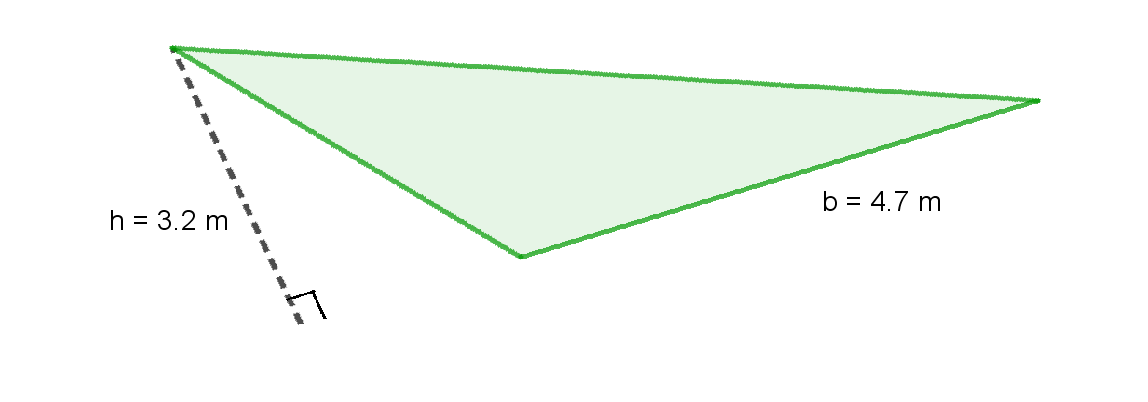
What is the area of a right-angled triangle with a base length of 3.2 m and a height of 4 m?

Question 2¶

What is the area of the triangle in question 1 if the height is halved?

Question 3¶

What is the area of the triangle in question 1 if the base is halved and the height is doubled?

Question 4¶

If the triangle in question 1 was an acute triangle instead of right angle triangle would the area be greater than, equal to, or less than the area as a right angle triangle?

What if you know the area, but not one of the variables?¶

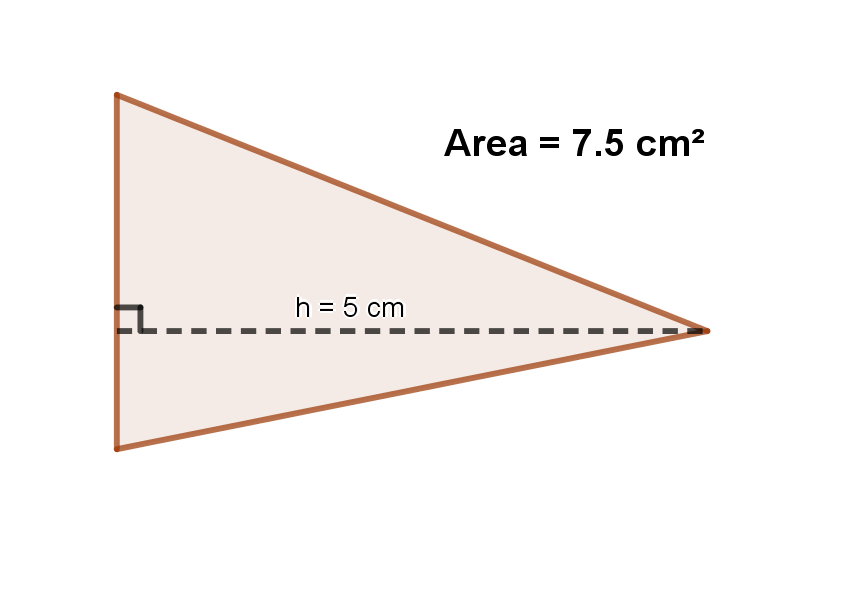
Let’s say you know the area and the base, but are asked for the height, or you know the area and the height, but are asked for the base. How can we find these missing variables? Look at this example below. What is the height of the triangle?

Image('images/TriQ4.png',width=300,height=200)

Let’s look at the formula:

\[ \text{Area of triangle} = \frac{\text{base} \times \text{height}}{2}\]

Now let’s plug in all the values we know into the formula:

\[11.2 \text{ mm}^2 = \frac{7 \text{ mm} \times \text{height}}{2}\]

This looks a lot different than when all the numbers we know are on one side of the equals sign, so let’s solve this equation for height which will put all the numbers on one side of the equals sign and height will be the only thing on the other side of the equals sign.

Don’t forget, to keep the meaning of the equation the same, any operation you do on one side, you must do it to the other.

\[\begin{split} \begin{align*} 11.2 \text{ mm}^2 & = \frac{7 \text{ mm} \times \text{height}}{2}\\ 11.2 \text{ mm}^2 \times 2 & = \frac{7 \text{ mm} \times \text{height}}{2\!\!\!\!\diagup}\times 2\!\!\!\!\diagup \tag{multiply by 2 to cancel out the division}\\[4pt] (11.2 \text{ mm}^2 \times 2) \div 7 \text{ mm} & = 7\!\!\!\!\diagup \text{ mm} \times \text{height} \div 7\!\!\!\!\diagup \text{ mm} \tag{divide by 7 mm to cancel out the base}\\[4pt] (11.2 \text{ mm}^2 \times 2) \div 7 \text{ mm} & = \text{height} \tag{Solve}\\[4pt] 22.4 \text{ mm}^2\!\!\!\!\diagup \div 7 \text{ mm}\!\!\!\!\diagup & = \text{height} \tag{cancel units}\\[4pt] 3.2 \text{ mm} & = \text{height} \end{align*} \end{split}\]

At the step with the comment “Solve” on it, that step actually shows us the formula for height when you know the base and area. Let’s remove the values from that step to see what the formula is in general:

\[\frac{\text{Area of triangle} \times 2}{\text{base}} = \text{height}\]

This can also be written with height on the left and the formula on the right:

\[\text{height} = \frac{\text{Area of triangle} \times 2}{\text{base}}\]

What about the other way?¶

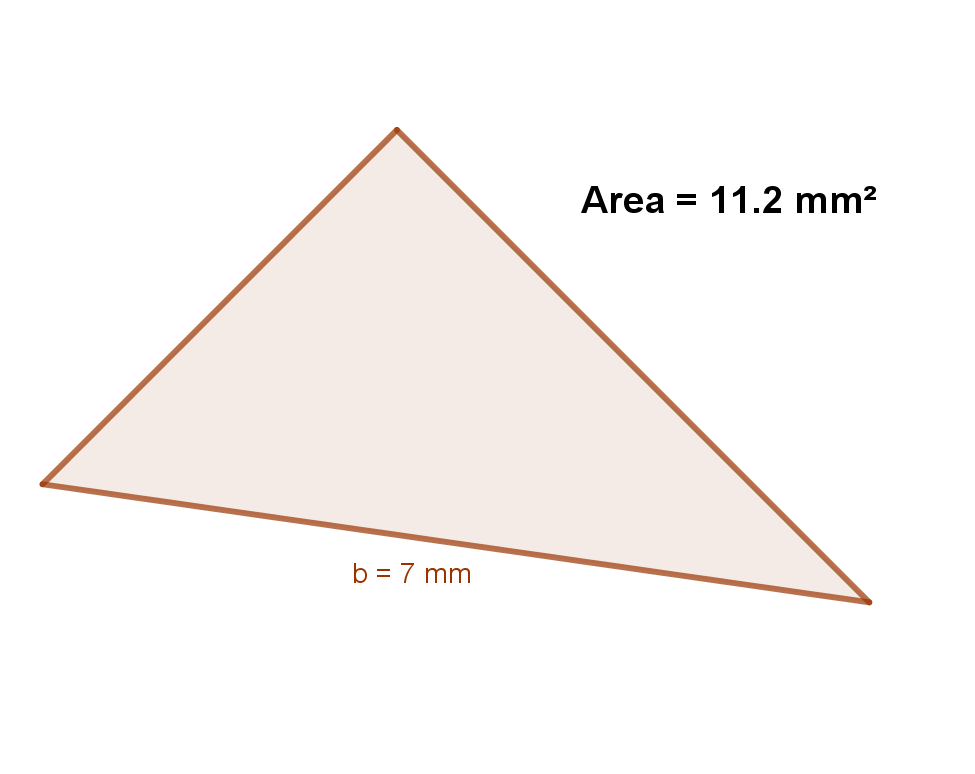
We can do the same thing if we know the height and not the base! What is the base length of this triangle?

Image('images/TriQ5.png',width=400,height=200)

Let’s use the same steps as the last example to solve this one.

Don’t forget, to keep the meaning of the equation the same, any operation you do on one side, you must do it to the other.

\[\begin{split} \begin{align*} \text{Area of triangle} & = \frac{\text{base} \times \text{height}}{2}\\ 7.5 \text{ cm}^2 & = \frac{\text{base} \times 5 \text{ cm}}{2} \tag{plug in values}\\[4pt] 7.5 \text{ cm}^2 \times 2 & = \frac{\text{base} \times 5 \text{ cm}}{2\!\!\!\!\diagup}\times 2\!\!\!\!\diagup \tag{multiply by 2 to cancel out the division}\\[4pt] (7.5 \text{ cm}^2 \times 2) \div 5 \text{ cm} & = \text{base} \times 5\!\!\!\!\diagup \text{ cm} \div 5\!\!\!\!\diagup \text{ cm} \tag{Divide by 5 cm to cancel out the base}\\[4pt] (7.5 \text{ cm}^2 \times 2) \div 5 \text{ cm} & = \text{base} \tag{Solve}\\[4pt] 15 \text{ cm}^2\!\!\!\!\diagup \div 5 \text{ cm}\!\!\!\!\diagup & = \text{base} \tag{cancel units}\\ 3 \text{ cm} & = \text{base} \end{align*} \end{split}\]

Now let’s get the general formula from the “Solve” step:

\[\frac{\text{Area of triangle} \times 2}{\text{height}} = \text{base}\]

This can also be written with base on the left and the formula on the right:

\[\text{base} = \frac{\text{Area of triangle} \times 2}{\text{height}}\]

Practice Questions¶

Try to figure out the values of the missing base or height.

Question 1¶

What is the height of this triangle?

Image('images/TriQ7.png',width=600)

ans4 = widgets.Text(value='',placeholder='0',description='Height =',continuous_update=False)

def display4():
    IPython.display.display(ans4)

def check4(a):
    IPython.display.clear_output(wait=True)
    display4()
    if ans4.value == '0.4 cm' or ans4.value == '0.4cm':
        print("Great job!")
    else:
        if ans4.value == '':
            pass
        if ans4.value == '0.4':
            print("Don't forget units!")
            print("You can include units in your answer by typing cm, m, or mm.")
        else:
            print("Not quite, don't forget the formula for height.")

display4()
ans4.observe(check4, 'value')

Question 2¶

What is the base length of this triangle?

Image('images/TriQ6.png',width=300)

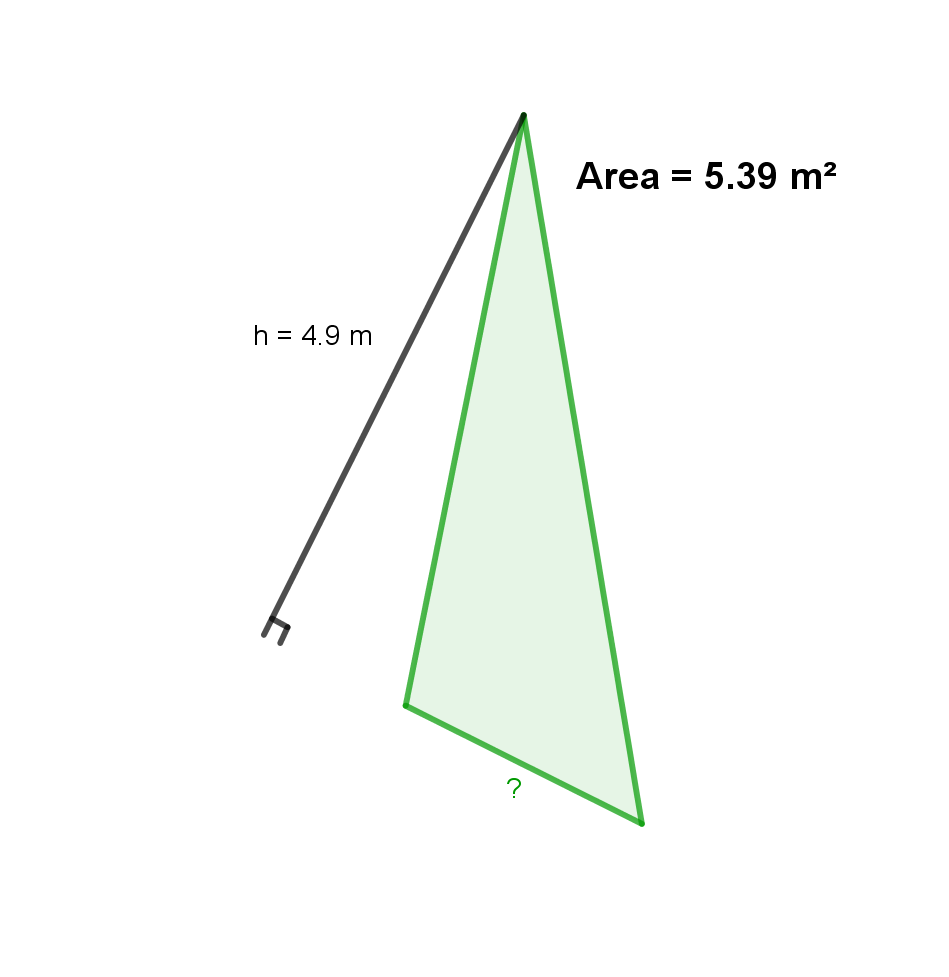
ans5 = widgets.Text(value='',placeholder='0',description='Base =',continuous_update=False)

def display5():
    IPython.display.display(ans5)

def check5(a):
    IPython.display.clear_output(wait=True)
    display5()
    if ans5.value == '2.2 m' or ans5.value == '2.2m':
        print("Great job!")
    else:
        if ans5.value == '':
            pass
        if ans5.value == '2.2':
            print("Don't forget units!")
            print("You can include units in your answer by typing cm, m, or mm.")
        else:
            print("Not quite, don't forget the formula for base length.")

display5()
ans5.observe(check5, 'value')

Question 3¶

What is the height of this triangle?

Image('images/TriQ8.png',width=300)

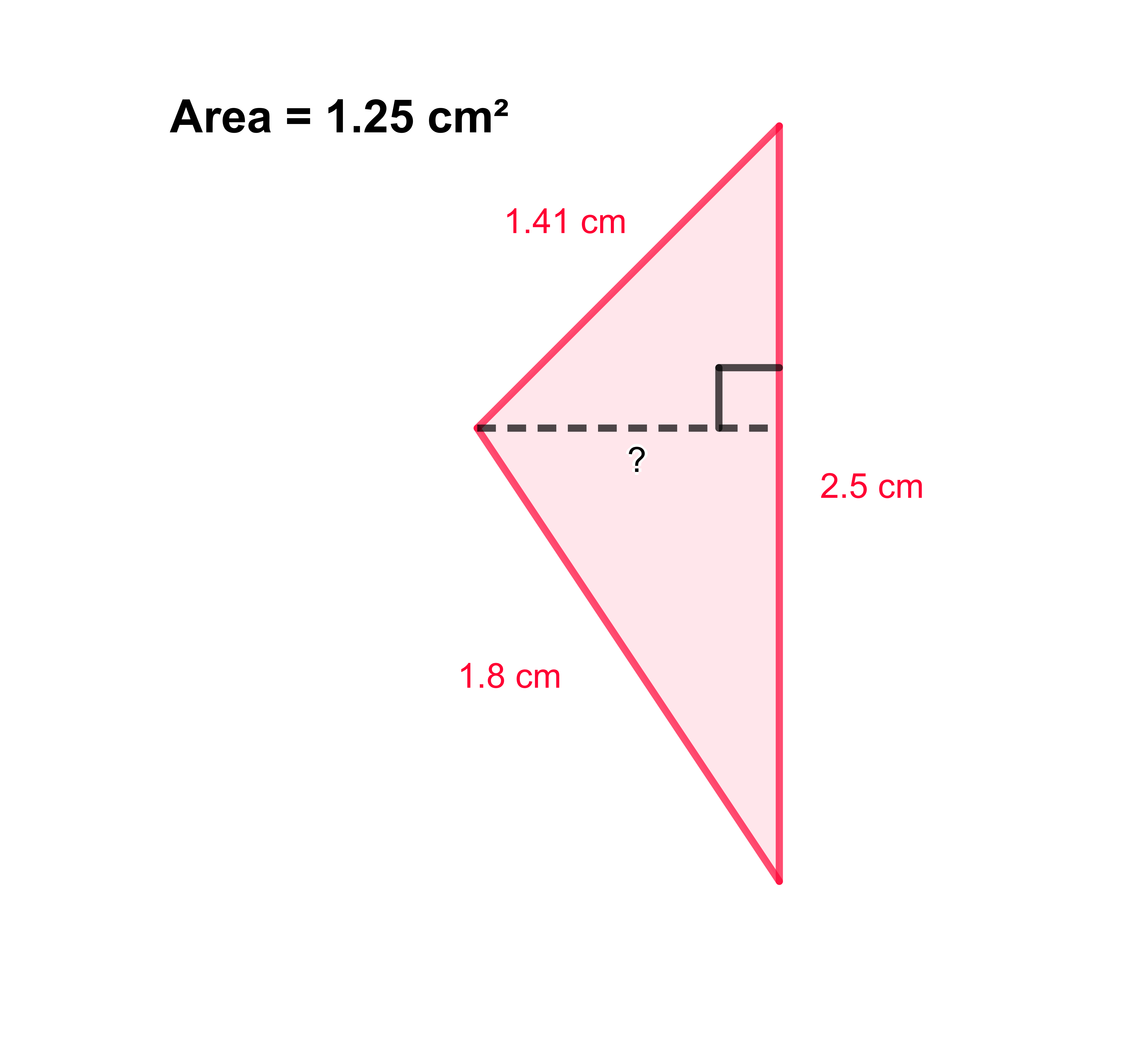
ans6 = widgets.Text(value='',placeholder='0',description='Height =',continuous_update=False)

def display6():
    IPython.display.display(ans6)

def check6(a):
    IPython.display.clear_output(wait=True)
    display6()
    if ans6.value == '1 cm' or ans6.value == '1cm':
        print("Great job!")
    else:
        if ans6.value == '':
            pass
        if ans6.value == '1':
            print("Don't forget units!")
            print("You can include units in your answer by typing cm, m, or mm.")
        else:
            print("Not quite, don't forget the formula for height.")

display6()
ans6.observe(check6, 'value')

What if you have other information other than the base and height?¶

There are lots of ways to calculate the area of a triangle with different information given to you, some even require knowing an angle or two in the triangle, but thats coming in the future. If you want to learn a little bit about another way to calculate area, this time knowing the length of all three sides, but not the height, then look at the article on Heron’s formula but you don’t have to know this yet.

Conclusion¶

Let’s review what we’ve learned in this notebook.

The area of a triangle is half the area of a rectangle with the same base and height.
The formula is \(\text{Area} = \frac{\text{base } \times \text{ height}}{2}\)
The formula works for all types of triangles as long as you know base and height.
The formula works for finding any variable that is missing by rearranging values on either side of the equals sign.
There’s more than one way to calculate the area.

Take the time to learn this formula and how to fill it in. You may not always have the formula to read, but filling in and manipulating equations like this formula will be essential for many math skills in the future. As always in mathematics, the more you practice, the easier it gets!

Callysto Curriculum Notebooks

Triangles: Area¶

Grade 7 Curriculum¶

What is a triangle?¶

How to find the area¶

What about non-right angle triangles?¶

Formula¶

Still not convinced?¶

Let’s try it with some numbers¶

Now let’s use our formula!¶

Question 1¶

Question 2¶

How does a change in height affect the area?¶

How does a change in base affect the area?¶

What conclusion can we draw?¶

Practice¶

Question 1¶

Question 2¶

Question 3¶

Question 4¶

What if you know the area, but not one of the variables?¶

What about the other way?¶

Practice Questions¶

Question 1¶

Question 2¶

Question 3¶

What if you have other information other than the base and height?¶

Conclusion¶