Fractions: Multiplication and Division¶

This is a notebook on how to multiply and divide by a fraction. In this notebook, you will learn how to multiply and divide between a whole number and a fraction, between two fractions, and between two mixed numbers.

This notebook starts with pictures to help you see how multiplying and dividing by a fraction changes a number. Then has a few practice questions at the end. (But remember that this one notebook will not be enough, you’ll need a lot more practice!)

If you don’t know what a numerator or denominator is, how to reduce fractions using common factors, or change a mixed number into a fraction then back again, please review those first before moving on to this notebook.

Multiplying a Whole Number with a fraction¶

We know that repeated addition can be written as multiplication with whole numbers, which are also know as integers, and we can do the same for fractions.

$\begin{align*} \frac15 + \frac15 + \frac15 & = \frac35 \\ 3 \times \frac15 & = \frac35 \end{align*}$

What if we want $4 \times \frac23$? Then we are saying we want two thirds of “4”, or 4 copies of two thirds, which is the same as eight copies of one-thirds, which is eight thirds. Lets look at what we did, but with numbers:

$\begin{align*} 4 \times \frac23 \\ 4 \times \frac23 & = 4 \times (2 \times \frac13) \\ 4 \times (2 \times \frac13) & = (4 \times 2) \times \frac13 \\ (4 \times 2) \times \frac13 & = 8 \times \frac13 \\ 8 \times \frac13 & = \frac83 \\ \frac83 & = 4 \times \frac23 \end{align*} $

Did you notice how we never had to find a common denominator? That’s because multiplication doesn’t need a common denominator!

Tip! To remember which fractions need the common denominator, think of this:

AS = Addition and Subtraction => Denominator needs to be All the Same

DM = Division and Multiplication => Denominator Doesn’t Matter

Multiplying two Fractions¶

Multiplying 2 fractions is taking a small piece from an already small piece. For example, we have half a bar of a candy bar and want to eat half of what we have, but we want to know how much of the whole candy bar we are going to be eating. This word problem describes $\frac{1}{2} \times \frac{1}{2}$ and we’ll learn how to solve this.

Visualizing multiplication of fractions¶

Let’s say we want to know what $\frac15 \times \frac12$ is equal to. Let’s show what’s going on using the rectangles below.

We cut our first rectangle vertically into 5 equal pieces, and select one of them (in blue) to show $\frac15$.
We cut our second rectangle horizontally into 2 equal pieces, and select one of them (in yellow) to show $\frac12$.

fig01 = plt.figure(figsize=(5,1))

t_data01 = [['','','','','']]
colors01 = [["b","w","w","w","w"]]
table01 = plt.table(cellText = t_data01,cellColours=colors01, loc='center')
table01.scale(1, 2)

plt.axis('off')
plt.grid('off')

fig02 = plt.figure(figsize=(5,1))

t_data02 = [[''],['']]
colors02 = [["yellow"],[ "w"]]
table02 = plt.table(cellText = t_data02,cellColours=colors02, loc='center')

plt.axis('off')
plt.grid('off')

plt.show()

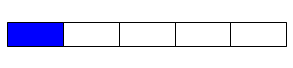
$../../../_images/multiplication-division-fractions_6_0.png$ $../../../_images/multiplication-division-fractions_6_1.png$

Now let’s lay one rectangle on top of the other. Do you see that there’s now 10 pieces, and only one is green? The green piece represents the product of this multiplication. Therefore: $\frac15 \times \frac12 = \frac{1}{10}$

fig = plt.figure(figsize=(5,1))

t_data = (('','','','',''), ('','','','',''))
colors = [["lime","yellow","yellow","yellow","yellow"],[ "b","w","w","w","w"]]
table = plt.table(cellText = t_data,cellColours=colors, loc='center')

plt.axis('off')
plt.grid('off')

plt.show()

$../../../_images/multiplication-division-fractions_8_0.png$

The next image shows that if we had done things the other way around, using a vertical cut for $\frac12$ and horizontal cuts for $\frac15$, the result is the same. This gives us a way of visualizing the fact that the order in which we multiply our fractions does not matter.

\[\frac15 \times \frac12 = \frac12 \times \frac15 = \frac{1}{10}\]

fig2 = plt.figure(figsize=(2,2))

t_data2 = (('',''), ('',''),('',''),('',''),('',''))
colors2 = [["lime","b"],[ "yellow","w"],[ "yellow","w"],[ "yellow","w"],[ "yellow","w"]]
table2 = plt.table(cellText = t_data2,cellColours=colors2, loc='center')

plt.axis('off')
plt.grid('off')

plt.show()

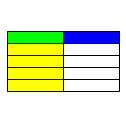
$../../../_images/multiplication-division-fractions_10_0.png$

Multiplying fractions¶

Method #1: sticking to the rules.¶

In this example, we will work out the product of two fractions using the rule of multiplying the numerators together, then the denominators together, then reducing the fraction if possible at the end.

What is the product of $\frac34\times\frac29$? Let’s walk through this step by step:

Step 1:¶

Multiply both numerators together to get the answer’s numerator.

In this question, the numerators are 3 and 2, so we get $3\times 2=6$ for the numerator of the product.

Step 2:¶

Multiply both denominators together to get the answer’s denominator.

In this question, the denominators are 4 and 9, so we get $4\times 9=36$ for the denominator of the product.

Step 3:¶

Reduce the fraction by dividing both the numerator and denominator by the greatest common factor (GCF). You already know how to do this!

Using the numbers from step 1 and step 2, we get $\frac34\times \frac29 = \frac{6}{36}$. But the GCF between 6 and 36 is not 1, it’s 6. So when we reduce by dividing the top and bottom by 6, we get a final answer of $\frac16$.

And You’re Done!¶

This method seems like the most straight-forward answer, but what if you need to calculate really big numbers like $\frac{5}{24} \times \frac{12}{13}$? You can use method #1, but then you need to do large multiplication, which is hard, and then you need to reduce after, which is also hard. But, there’s a way to make it easier! What if you reduce the fraction before doing the multiplication? That’s where method #2 comes in.

Method #2: A little less work.¶

The second approach relies on the fact that order of multiplication doesn’t matter, and that this is true not only for the product of the fractions, but for the products in the numerator and denominator as well! In other words, we are reducing the fraction before multiplying. Observe:

\[\begin{split}\hskip-36pt\begin{align*} \frac34\times \frac29 &= \frac{3\times 2}{4\times 9}\hspace{0.5cm} \text{Use the rule of Method #1}\\[5pt] &= \frac{2\times 3}{4\times 9} \hspace{0.5cm}\text{Change the order of multiplication in the numerator}\\[5pt] &= \frac24\times\frac39 \hspace{0.5cm}\text{The rule of Method #1, in reverse}\\[5pt] &= \frac12\times\frac13 \hspace{0.5cm}\text{Reduce fractions}\\[5pt] &= \frac{1\times 1}{2\times 3}= \frac16 \hspace{0.5cm}\text{Multiplying one more time} \end{align*}\end{split}\]

This might seem like more work (certainly, there are more steps), but what it tells us is that we can cancel between fractions. Let’s repeat the above calculation, using this shortcut:

$\hskip-60pt\large \frac34\times\frac29 = \frac{^{\color{red}{1}}3\!\!\!\!\diagup}{_{\color{blue}{2}}\,4\!\!\!\!\diagup}\times\frac{2\!\!\!\!\diagup^{\,\,\color{blue}{1}}}{9\!\!\!\!\!\diagup_{\,\,\color{red}{3}}} = \frac{1\times 1}{2\times 3}=\frac16.$

What we’ve done here is cancel the 3 in $\frac34$ with a factor of 3 in the $9=3\times 3$ in $\frac29$, and similarly, the 2 in $\frac29$ with the 4 in $\frac34$. The advantage of this approach is that the numbers we need to multiply are smaller, and (usually, if you were careful) no further reduction is needed. To recap:

Step 1:¶

Reduce fractions first, and you can reduce the numerator of one fraction with the denominator of the other by the same common factor.

Step 2:¶

Multiply both numerators together for the answer’s numerator. Multiply both denominators together for the answer’s denominator.

Step 3:¶

Though the fraction should already be reduced, check again in case it can be reduced again. Check to see if there’s any other common factors.

And You’re Done!¶

Let’s do another example. This time, we multiply an integer, a whole number, by a fraction. Remember that any integer, or whole number, can be written as a fraction with a denominator equal to 1. First, we will use Method #1.

\[\begin{split}\hskip-60pt\begin{align*} \frac{4}{7} \times 7 & = \frac{4}{7} \times \frac{7}{1} \tag{Turn integer into fraction}\\[5pt] \frac{4}{7} \times \frac{7}{1} & = \frac{28}{7} \tag{Multiply numerators and denominators}\\[5pt] \frac{28}{7} & = 4 \tag{Reduce the fraction}\\ \end{align*}\end{split}\]

Here’s the same example again, but this time, using the second method:

\[\begin{split}\hskip-60pt\begin{align*} \frac{4}{7} \times 7 & = \frac{4}{7} \times \frac{7}{1} \tag{Turn integer into fraction}\\[5pt] \frac{4}{7\!\!\!\!\diagup} \times \frac{7\!\!\!\!\diagup}{1} & = \frac{4}{1} \times \frac{1}{1} \tag{Reduce numbers}\\[5pt] \frac{4}{1} \times \frac{1}{1} & = 4 \tag{Multiply numerators and denominators} \end{align*}\end{split}\]

Let’s try one more example:

\[\begin{split}\hskip-60pt\begin{align*} \frac{4}{9} \times \frac{3}{5}\\ \frac{4}{9\!\!\!\!\diagup} \times \frac{3\!\!\!\!\diagup}{5} & = \frac{4}{3} \times \frac{1}{5} \tag{Reduce numbers}\\ \frac{4}{3} \times \frac{1}{5} & = \frac{4}{15} \tag{Multiply numerators and denominators} \end{align*}\end{split}\]

Here’s an animation showing the two methods on the same problem.¶

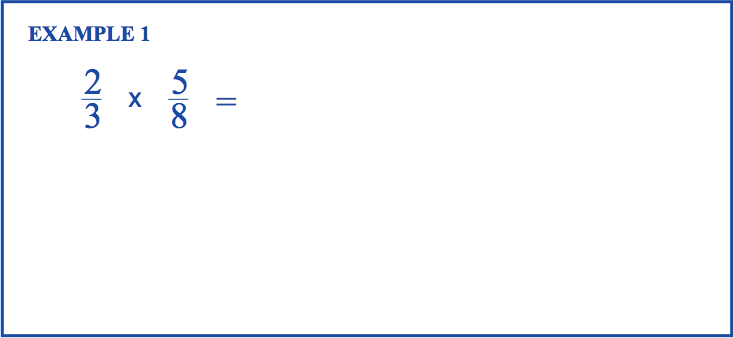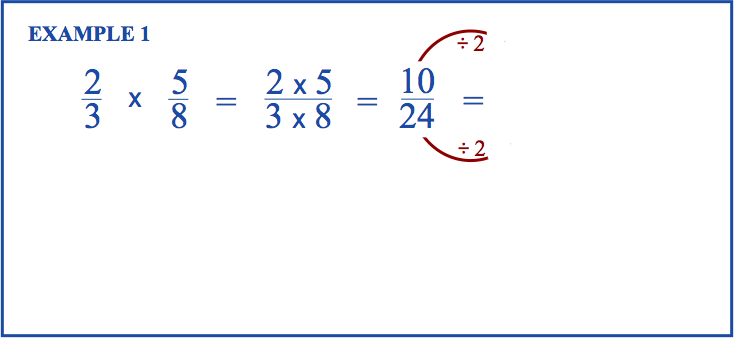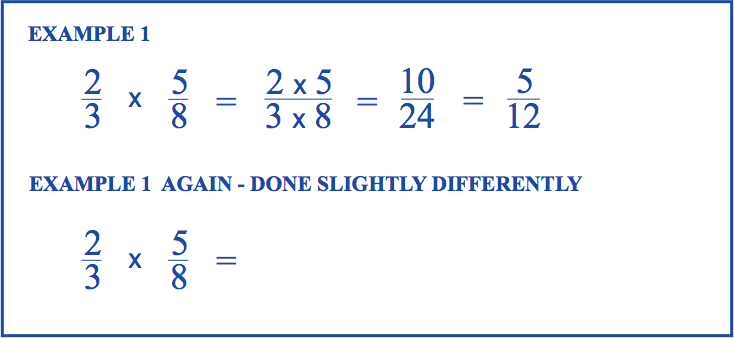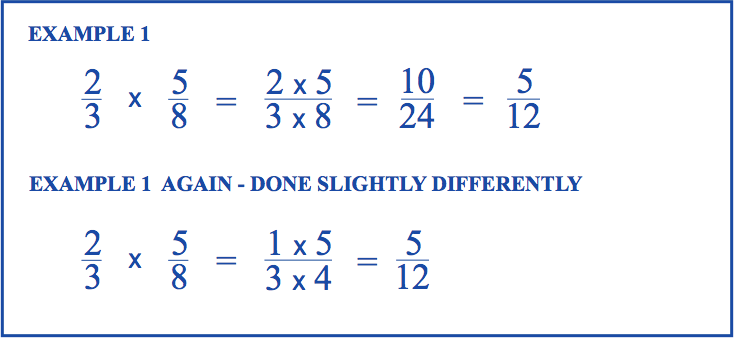
animation

Practice with fraction multiplication¶

It’s time to try a few exercises.

In the following problems, fill in the missing numbers with integers. (Whole numbers.) Watch out for reductions!

$$\hskip-60pt\frac{2}{7} \times \frac{3}{5} = \frac{6}{\color{Red}{a}}$$

a = widgets.IntText(value=0, description='a =', disabled=False)

IPython.display.display(a)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(a)
    if a.value == 35:
        print("That's right! Great work!")
    else:
        if a.value == 0:
            pass
        else:
            print("Sorry, try again (and it was not a reducing error)")

a.observe(check, 'value')

\[\hskip-60pt\frac{4}{9} \times \frac{1}{10} = \frac{\color{Blue}{b}}{45}\]

b = widgets.IntText(value=0, description='b =', disabled=False)

IPython.display.display(b)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(b)
    if b.value == 2:
        print("That's right! Great work!")
    else:
        if b.value == 0:
            pass
        if b.value == 4:
            print("Not quite, don't forget to reduce.")
        else:
            print("Sorry, try again (and it was not a reducing error)")

b.observe(check, 'value')

\[\hskip-60pt\frac{2}{3} \times \frac{9}{10} = \frac{\color{Purple}{c}}{\color{Green}{d}}\]

c = widgets.IntText(value=0, description='c =', disabled=False)

IPython.display.display(c)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(c)
    if c.value == 3:
        print("That's right! Great work!")
    else:
        if c.value == 0:
            pass
        if c.value == 18 or c.value == 9 or c.value == 6:
            print("Not quite, don't forget to reduce.")
        else:
            print("Sorry, try again (and it was not a reducing error)")

c.observe(check, 'value')

d = widgets.IntText(value=0, description='d =', disabled=False)

IPython.display.display(d)
def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(d)
    if d.value == 5:
        print("That's right! Great work!")
    else:
        if d.value == 0:
            pass
        if d.value == 30 or d.value == 15 or d.value == 10:
            print("Not quite, don't forget to reduce.")
        else:
            print("Sorry, try again (and it was not a reducing error)")

d.observe(check, 'value')

Dividing Positive Fractions¶

How do we divide using fractions?¶

If you know how to multiply fractions, then you already know how to divide fractions!

Let’s go back to dividing integers,or whole numbers. We know that 10 divided by 2 is 5, because 10 can be split into 2 portions each of which has 5. Now notice that dividing 10 by 2 is the same as taking half of 10. That is,

$10\div2 = 10\times \frac12 = 5.$

Notice that in the equality $10 \div 2 = 10\times\frac{1}{2}$, we took the reciprocal of the second number ($\frac{2}{1} \rightarrow \frac{1}{2}$) then changed the division to multiplication! What is the reciprocal? It’s when the old numerator becomes the new denominator and the old denominator becomes the new numerator!

That’s how division with fractions works too: flip the divisor, the number after the division, and then multiply!

The golden rule of division: division is the same as multiplying by the reciprocal¶

For example, what is $10\div \frac{1}{3}$? If we apply the rule we just came up with, we find

$10\div \frac13 = 10\times\frac31 = 10\times 3 = 30.$

Does this make sense? Recall that when we compute $10\div 2=5$, what we’re working out is the number of groups of 2 we need to make 10. Similarly, the expression $10\div \frac13$ is asking how many $\frac{1}{3}$ pieces can fit into 10 pieces. Since it takes 3 $\frac{1}{3}$s to make one and 10 ones to make 10, we need $3\times 10 = 30$ pieces of size $\frac{1}{3}$ to make 10, therefore $10 \div \frac{1}{3} = 10 \times 3 = 30$.

Here are the steps¶

Step 1:¶

Find the reciprocal of the divisor. (By making the numerator the denominator and the denominator the numerator of the second fraction.)

Step 2:¶

Follow the steps to multiply the fractions using either method mentioned earlier.

And you’re done!¶

Tip! To remember these steps to divide fractions, think of this:

KFC:

K is for Keep the first fraction the same

F is for Flip the second fraction

C is for Change the sign from divide to multiply

But why does this work?¶

Remember that division is the opposite of multiplication: dividing by a number “undoes” multiplication by that same number. This has a special name, division is the inverse operation of multiplication. Here, we are interested in undoing multiplication by fractions. Let’s start with an integer example. Consider the multiplication of 10 by 4: $10 \times 4 = 40$. To undo the multiplication by 4, we divide by 4: $40 \div 4 = 10$ and we get back to the original number! Same goes for fractions: consider the product $20 \times \frac{1}{2} = 10$. Dividing by $\frac12$ should undo the multiplication. Our rule for division says that to divide by $\frac{1}{2}$, we multiply by $\frac21 = 2$: $10 \div \frac{1}{2} = 10\times 2 = 20$. Once again, we get back to the original number!

If dividing by 4 is equivalent to multiplying by $\frac{1}{4}$, then it’s true that dividing by $\frac{1}{4}$ is equivalent to multiplying by 4.

What if you flip the first number instead of the second? Try it with an example we’ve already solved. Does it change the answer or does the order not matter like multiplication?

But isn’t division supposed to make the number smaller?¶

The short answer is, “Yes, but only if the number we’re dividing by is bigger than 1.” Try thinking of division as repeated subtraction: $2 \div \frac{1}{2}$ is asking how many times can we subtract $\frac{1}{2}$ from 2.

\[\begin{split}\hskip-60pt \begin{align*} 2 - \frac{1}{2} &= 1\frac{1}{2}\tag{once}\\[5pt] 1\frac{1}{2} - \frac{1}{2} &= 1\tag{twice}\\[5pt] 1 - \frac{1}{2} &= \frac{1}{2}\tag{three times}\\[5pt] \frac{1}{2} - \frac{1}{2} &= 0\tag{four times} \end{align*}\end{split}\]

So it took 4 subtractions of $\frac{1}{2}$ from 2 to reach 0, therefore $2 \div \frac{1}{2} = 4$.

This is because we are taking smaller portions out of the original number, so we need more subtractions to get to zero.

Here’s another example. In this example, we perform division by multiplying by the reciprocal, and we use Method #2, reducing our fractions before carrying out the multiplication.
$$\hskip-36pt\large \frac14\div\frac38 = \frac14\times\frac83 = \frac{1}{_{\color{red}{1}}\,4\!\!\!\!\diagup}\times\frac{8\!\!\!\!\diagup^{\,\,\color{red}{2}}}{3} = \frac23.$$

Still need another explanation? Here’s a video that might help:

from IPython.display import YouTubeVideo
YouTubeVideo('f3ySpxX9oeM')

Let’s go through an example:¶

\[\begin{split}\hskip-60pt\begin{align*} \color{blue}{\frac{4}{5} \div \frac{2}{7}}\\ \frac{4}{5} \div \frac{2}{7} & = \frac{4}{5} \times \frac{7}{2} \tag{Invert the divisor}\\ \frac{4\!\!\!\diagup}{5} \times \frac{7}{2\!\!\!\diagup} & = \frac{2}{5} \times \frac{7}{1} \tag{Reduce numbers}\\ \frac{2}{5} \times \frac{7}{1} & = \frac{14}{5} \tag{Multiply numerators and denominators}\\ \frac{14}{5} & = 2 \frac{4}{5} \tag{Write as a mixed fraction} \end{align*}\end{split}\]

Here’s a fill in the blank question. Please read which numbers need to be filled out correctly, and then enter the correct values below.

\[\hskip-60pt\frac{2}{3} \div \frac{5}{7} = \frac{2}{3} \times \frac{\color{Blue}{A}}{\color{Green}{B}} = \frac{\color{Purple}{C}}{\color{Red}{D}}\]

A = widgets.IntText(value=0, description='A =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(A)
    if A.value == 7:
        print("That's right! Great work!")
    else:
        if A.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(A) 
A.observe(check, 'value')

B = widgets.IntText(value=0, description='B =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(B)
    if B.value == 5:
        print("That's right! Great work!")
    else:
        if B.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(B)
B.observe(check, 'value')

C = widgets.IntText(value=0, description='C =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(C)
    if C.value == 14:
        print("That's right! Great work!")
    else:
        if C.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(C)
C.observe(check, 'value')

D = widgets.IntText(value=0, description='D =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(D)
    if D.value == 15:
        print("That's right! Great work!")
    else:
        if D.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(D)
D.observe(check, 'value')

Here’s another fill in the blank question. Please read which numbers need to be filled out correctly.
Note: there is a reduction in this one!

\[\hskip-60pt\frac{4}{9} \div \frac{5}{3} = \frac{4}{9} \times \frac{3}{5} = \frac{4}{\color{Blue}{E}} \times \frac{\color{Green}{F}}{5} = \frac{\color{Purple}{G}}{\color{Red}{H}}\]

E = widgets.IntText(value=0, description='E =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(E)
    if E.value == 3:
        print("That's right! Great work!")
    else:
        if E.value == 0:
            pass
        if E.value == 9:
            print("Don't forget to reduce.")
        else:
            print("Sorry, try again.")
            
IPython.display.display(E) 
E.observe(check, 'value')

F = widgets.IntText(value=0, description='F =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(F)
    if F.value == 1:
        print("That's right! Great work!")
    else:
        if F.value == 0:
            pass
        if F.value == 3:
            print("Don't forget to reduce.")
        else:
            print("Sorry, try again.")
            
IPython.display.display(F) 
F.observe(check, 'value')

G = widgets.IntText(value=0, description='G =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(G)
    if G.value == 4:
        print("That's right! Great work!")
    else:
        if G.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(G) 
G.observe(check, 'value')

H = widgets.IntText(value=0, description='H =', disabled=False)

def check(q):
    IPython.display.clear_output(wait=False)
    IPython.display.display(H)
    if H.value == 15:
        print("That's right! Great work!")
    else:
        if H.value == 0:
            pass
        else:
            print("Sorry, try again.")
            
IPython.display.display(H) 
H.observe(check, 'value')

Multiplication and Division with Positive Mixed Fractions¶

With mixed numbers, we have to do a little more work, but it’s only one more step:

For multiplication and division, all mixed numbers must be converted to improper fractions.¶

This notebook is assuming that you already know how to convert between mixed numbers and improper fractions

Remember that a mixed number is really adding an integer and a proper fraction: $3\,\frac14$ is really $3+\frac14$ as one number. A proper fraction is where the numerator is less than the denominator. An improper fraction is where the numerator is bigger than or equal to the denominator.

For example, consider the product $\frac45\times 3\,\frac14$. So one way to carry out the product is to use the distributive property:

\[\begin{split}\hskip-60pt\begin{align*} \frac45 \times 3\,\frac14 &= \frac45(3+\frac14)\\ & = \frac45\times 3+\frac45\times\frac14\\ &= \frac{12}{5}+\frac15\\ &= \frac{13}{5}. \end{align*}\end{split}\]

(Note that we’ve made use of two skills practised above, without writing them down: we multiplied by 3 by thinking of it as the fraction $\frac31$, and we cancelled the fours in the product $\frac45\times \frac14$.)

If it is asked for, we can do one final step, and convert back to a mixed fraction: $\dfrac{13}{5} = 2\,\dfrac{3}{5}$. But that was quite a bit of work. There must be a better way!

Instead, let’s first convert our mixed number to an improper fraction:

\[3\,\frac14 = 3+\frac14 = 3\times\frac44+\frac14 = \frac{12}{4}+\frac{1}{4} = \frac{13}{4}.\]

Now we can multiply using the methods we learned above:

\[\frac45\times 3\,\frac14 = \frac45\times\frac{13}{4} = \frac15\times\frac{13}{1}=\frac{13}{5},\]

as before. If specified in the problem (or by your teacher), you can take one more step and convert the improper fraction $\frac{13}{5}$ into the mixed number $2\,\frac35$.

Let’s review the steps:

Step 1:¶

$\color{red}{\textrm{Convert all mixed numbers into improper fractions.}}$

Step 2:¶

Multiply or divide as using the methods earlier.

Step 3: (Optional?)¶

If the result is an improper fraction, convert it back to a mixed number.

And you’re done!¶

Let’s do some examples!¶

Calculate the product $\color{blue}{2 \dfrac{2}{3} \times 1 \dfrac{3}{4}}$.

$\hskip-60pt\begin{align*} 2 \frac{2}{3} \times 1 \frac{3}{4} & = \frac{8}{3} \times \frac{7}{4} \tag{Convert to improper fractions}\\[5pt] \frac{8\!\!\!\diagup}{3} \times \frac{7}{4\!\!\!\diagup} & = \frac{2}{3} \times \frac{7}{1} \tag{Reduce numbers}\\[5pt] \frac{2}{3} \times \frac{7}{1} & = \frac{14}{3} \tag{Multiply numerators and denomintators}\\[5pt] \frac{14}{3} & = 4 \frac{2}{3} \tag{Write as a mixed fraction} \end{align*}$
Calculate the quotient $\color{blue}{2 \dfrac{2}{3} \div 1 \dfrac{3}{4}}$. (These are the same fractions as the first example.)

$\hskip-60pt\begin{align*} 2 \frac{2}{3} \div 1 \frac{3}{4} & = \frac{8}{3} \div \frac{7}{4} \tag{Convert to improper fractions}\\[5pt] \frac{8}{3} \div \frac{7}{4} & = \frac{8}{3} \times \frac{4}{7} \tag{Invert the divisor}\\[5pt] \frac{8}{3} \times \frac{4}{7} & = \frac{32}{21} \tag{Multiply numerators and denomintators}\\[5pt] \frac{32}{21} & = 1 \frac{11}{21} \tag{Write as a mixed fraction} \end{align*}$
Calculate the quotient $\color{blue}{3 \frac{1}{2} \div 1 \frac{1}{6}}$. (This time some reduction is required.)

$\hskip-60pt\begin{align*} 3 \frac{1}{2} \div 1 \frac{1}{6} & = \frac{7}{2} \div \frac{7}{6} \tag{Convert to improper fractions}\\[5pt] \frac{7}{2} \div \frac{7}{6} & = \frac{7}{2} \times \frac{6}{7} \tag{Invert the divisor}\\[5pt] \frac{7\!\!\!\diagup}{2} \times \frac{6}{7\!\!\!\diagup} & = \frac{1}{2} \times \frac{6}{1} \tag{Reduce numbers}\\[5pt] \frac{1}{2\!\!\!\diagup} \times \frac{6\!\!\!\diagup}{1} & = \frac{1}{1} \times \frac{3}{1} \tag{Reduce numbers again}\\[5pt] \frac{1}{1} \times \frac{3}{1} & = \frac{3}{1} \tag{Multiply numerators and denomintators}\\[5pt] \frac{3}{1} & = 3 \tag{Write as an integer} \end{align*}$

Practice Questions¶

Now that you’ve seen a few examples, it’s time to try some on your own. But remember: two problems worth of practice is not enough to master this skill. Make sure you take the time to work through additional problems from your teacher or textbook.

Grab some extra paper and a pencil to go through the steps in this notebook to find the answer, then check to see if you’re right.

Question 1¶

$2\frac{1}{2} \times 1\frac{1}{2}$

from fractions import Fraction

answer = widgets.RadioButtons(options=['','3 3/4', '2 1/4','4','1 2/3'],
                              value='', description= 'Answer')

def check(a):
    IPython.display.clear_output(wait=False)
    IPython.display.display(answer)
    if answer.value == '3 3/4':
        print("Correct! Great job!")
    else:
        if answer.value == '':
            pass
        else:
            print("Sorry, that's not right, try again. Don't forget to convert the fraction to an improper fraction.")

IPython.display.display(answer)
answer.observe(check, 'value')

Question 2¶

$3\frac{1}{3} \div 2\frac{1}{6}$

answer2 = widgets.RadioButtons(options=['','7 2/9', '2 1/2','1 7/13','3 1/2'],
                              value='', description= 'Answer')

def check(a):
    IPython.display.clear_output(wait=False)
    IPython.display.display(answer2)
    if answer2.value == '1 7/13':
        print("Correct! Great job!")
    else:
        if answer.value == '':
            pass
        else:
            print("Sorry, that's not right, try again. Don't forget to convert the fraction to an improper fraction and invert the divisor.")

IPython.display.display(answer2)
answer2.observe(check, 'value')

Summary¶

Let’s review what we’ve learned in this notebook.

Unlike addition, multiplying fractions does not need common denominators. DM – Division/Multiplication = Denominator Doesn’t Matter
To multiply to fractions, multiply the numerators, then the denominators, and then reduce if necessary.
It is often easier if you cancel common factors before multiplying the fractions.
Division is the inverse of multiplication. Remember the Golden Rule: division is the same as multiplying by the reciprocal! (flipping the numerator and denominator) KFC - Keep, Flip, Change
Multiplication and division involving mixed numbers is easier if you first convert any mixed numbers to improper fractions.

Take the time to master your fraction multiplication and division. It may not seem like it now, but this is a much needed skill that you’ll rely on for many years to come. Many careers even use fractions on a daily basis, like chefs or construction workers. As always in math, the more you practice, the easier it gets!

Callysto Curriculum Notebooks

Fractions: Multiplication and Division¶

Multiplying a Whole Number with a fraction¶

Multiplying two Fractions¶

Visualizing multiplication of fractions¶

Multiplying fractions¶

Method #1: sticking to the rules.¶

Step 1:¶

Step 2:¶

Step 3:¶

And You’re Done!¶

Method #2: A little less work.¶

Step 1:¶

Step 2:¶

Step 3:¶

And You’re Done!¶

Here’s an animation showing the two methods on the same problem.¶

Practice with fraction multiplication¶

Dividing Positive Fractions¶

How do we divide using fractions?¶

The golden rule of division: division is the same as multiplying by the reciprocal¶

Here are the steps¶

Step 1:¶

Step 2:¶

And you’re done!¶

But why does this work?¶

But isn’t division supposed to make the number smaller?¶

Let’s go through an example:¶

Multiplication and Division with Positive Mixed Fractions¶

For multiplication and division, all mixed numbers must be converted to improper fractions.¶

Step 1:¶

Step 2:¶

Step 3: (Optional?)¶

And you’re done!¶

Let’s do some examples!¶

Practice Questions¶

Question 1¶

Question 2¶

Summary¶