Order of Operations¶

Grade 9 curriculum¶

A Jupyter notebook to explore order of operations conventions for arithmetic operations.

Introduction¶

In elementary mathematics, we have two basic operations: addition and multiplication. Each of these operations comes with an “opposite” (or, as a mathematician might say, an inverse) operation. The opposite of addition is subtraction, and the opposite of multiplication is division.

When there is a single operation to perform, we all know what to do, including the computer. For example, we could have the computer calculate the sum \(3+7\) or the product \(9\times 3\):

3+7

9*3

If you want to type your expressions into an input box, the operators are:

Brackets: ( and )
Exponents: **
Division: /
Multiplication: *
Addition: +
Subtraction: -

Note: all code in Jupyter is live, and editable. Feel free to go back to the last two lines and change the numbers. To get the computer to do the calculation, press Shift+Enter on your keyboard.

If we wanted to undo either the addition or the multiplication, we can use their opposites:

10-7

27/3

9.0

You might be wondering why there is a decimal in the last output. Whenever the computer does division, it uses floating point arithmetic, and it is allowing for the fact that division doesn’t always return a whole number.

Now, if we need to add up a whole bunch of numbers (or multiply them), we don’t have to worry about doing it wrong, thanks to a property of arithmetic called associativity. Basically, it means if we want to compute a sum like \(5+9+7\), it doesn’t matter if we first do \(5+9\), and then add 7, or if we do \(9+7\) and then add 5. In other words, it doesn’t matter if we first associate 5 with 9, or associate 9 with 7—both ways give us the same result. (Because of this, we say addition is associative.) To distinguish between the two associations, we use parentheses like this:

\[(5+9)+7 = 5+(9+7)\]

In mathematics, using brackets (or parentheses) is a way of saying, “Do this first!”

Go ahead and try this for yourself. Then, let the computer confirm it for you. We’ve entered the left-hand side of the above equality for you. To try the right-hand side, click on the \(+\) sign in the tool bar at the top to add a new cell. Type in the right-hand side yourself, and press Shift+Enter to confirm the result.

(5+9)+7

The same thing works for multiplication. For example, \((2\cdot 4)\cdot 5 = 40 = 2\cdot (4\cdot 5)\). And of course, as well as being able to put brackets wherever we want, we can also change the order of the numbers without affecting the answer.

Things get more complicated if we want to do both addition and multiplication in a single calculation, or if we want to bring subtraction or division into the picture. Consider this expression:

\[3+7\times 4\]

Which operation should we do first? The addition, or the multiplication? Or does it matter? Let’s try both ways using parentheses; as noted above, any operation in parentheses is always done first. We see the results in the two cells below:

(3+7)*4

3+(7*4)

Interesting! Order doesn’t matter when there’s only addition or only multiplication involved, but as soon as we combine the two, the order (and hence, the placement of brackets) does make a difference.

Exercise¶

Does order matter for subtraction or division? Let’s see by using brackets again. In the code cells below, try a few examples to see what happens. We’ve done a couple for you to show you how they’re written. Note that you can do more than one calculation in a cell by using a comma to separate them.

(10-3)-5, 10-(3-5)

(2, 12)

(12/6)/2, 12/(6/2)

(1.0, 4.0)

The Problem¶

How do we (or a computer) figure out the answer to a really complicated expression like this?

\[8 + 5/3^{2} \times (7 - 4)/(6 + 9)\]

The answer is the same for both humans and computers: we need to

Break the problem down into simpler steps, and
Determine the order in which those steps should be performed.

We know what the simpler steps should be; these are the individual arithmetic operations. How do we determine the order? The short answer is that there is an agreed-upon convention. In other words, everybody agrees to do operations in the same order so that they always get the same answer. This order is called (conveniently) the order of operations.

The Order of Operations is:¶

Brackets
Exponents
Division
Multiplication
Addition
Subtraction

This is commonly remembered by the acronym BEDMAS, or PEMDAS (if we use the word “parentheses” instead of “brackets”) or even BODMAS (if we use “orders” instead of “exponents”). Some people remember this order by the phrase Please Excuse My Dear Aunt Sally.

Did you notice? the D and M in PEMDAS are switched around! Doesn’t that change things? (The answer is coming up!)

Here’s a way to visualize the order of operations. Higher operations are done first.

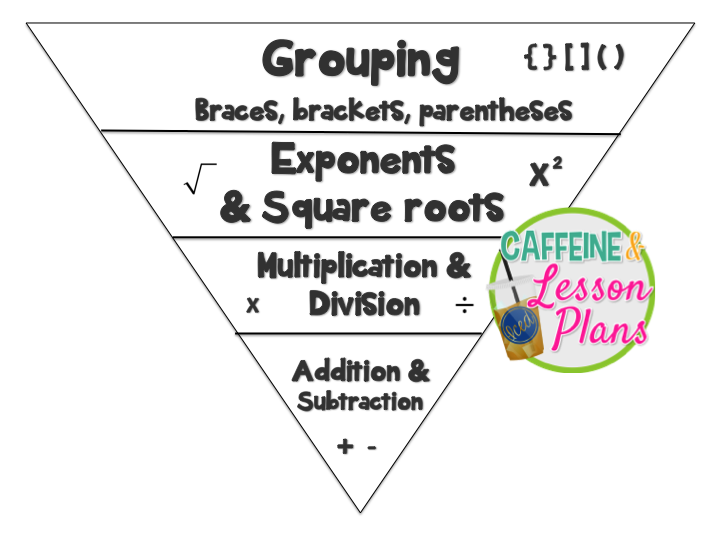
Pyramid

What happens if there are multiple operations on the same level of the pyramid?¶

This means they have the same amount of importance, and so they’re treated as if they were the same operation. (Technically, it means they are the same operation—ask your teacher why!) In other words, we do multiplication and division at the same time, left-to-right, then we do addition and subtraction at the same time, left-to-right.

But why do we have the order of operations? And why not a different order?¶

The short answer is because all operations boil down to addition and subtraction. It’s true: exponents are repeated multiplication, and multiplication itself is repeated addition. So we want to do the most complex operations first before moving on to the simpler ones. Brackets are used to show associations that might break this order, which is why they must be done first.

The long answer can be found here: http://mathforum.org/library/drmath/view/52582.html

Let’s try a simple calculation with two operations. If we want to explicitly tell the computer which operation to perform first, we can use brackets. First, we try doing the addition first:

(3 + 5) * 6

Next, let’s see what we get if we do the multiplication first:

3 + (5 * 6)

Finally, let’s input the expression without any brackets, and let the computer take care of the order.

3 + 5 * 6

What was the result? Did it match either of the calcuations above it? Based on this example, does it appear as though the computer is following the order of operations?

Are all computer programs created equal? Here are two calculators, from the same company, with the same input, but different outputs! Based on the BEDMAS order, which answer is right?

Note: 2(2+1) is the same as 2x(2+1), it’s just a different way to write it.

Can you figure out how to add additional brackets to reproduce each result?

Example¶

How do we evaluate the expression \(2^3 \times (4 + 8)\)?

Solution¶

Here is a step-by-step walk-through of the calculation:

\[\begin{split}\begin{align*} 2^3 \times \mathbf{(4+8)} & = 2^3\times 12 \tag{Brackets first!}\\ \mathbf{2^3}\times 12 & = 8\times 12 \tag{Exponents come next}\\ \mathbf{8\times 12} & = 96 \tag{Finally, the multiplication} \end{align*}\end{split}\]

On the computer, we expect the following steps to be carried out:

2^3 \(\times\) (4 \(+\) 8)

2^3 \(\times\) 12

8 \(\times\) 12

96

Let’s check to see if it works:

2**3 * (4 + 8)

Want to see another example? Watch this and try to solve it before they get to the solution!

%%html
<iframe width="560" height="315" src="https://www.youtube.com/embed/Y3CZ_JBQ0do?rel=0&amp;start=17" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>

Mixing things up¶

Let’s start with a number and 3 operations that can be applied to the number:

5

_ x 4

_ + 7

_ ^ 2

Let’s say we want to do the addition, then the exponent, then the multiplication. What’s the answer?

5 + 7 = 12 12^2 = 144 144 x 4 = 576

The answer is 576. But if we type the same series of operations into the computer, what do we get?

5+7**2*4

That’s not what we want! But we shouldn’t expect it to be: order of operations requires that the addition be performed last, not first!

Exercise:¶

Re-enter the above expression in the cell below, and then add brackets as needed to get the correct order of operations. Be sure that your output matches the correct answer!

What output do we get by doing the exponent, then the addition, then the mulitplication?

5^2 = 25 25 + 7 = 32 32 x 4 = 128

How can we write these expressions in one line to get this output?

Were you able to get 128 as your answer? Again, we see that the brackets are necessary. If we leave them out, then the computer follows the order of operations convention, and we get:

5**2+7*4

Can you think of another order to write these operations in that gives a different output?

Practice Questions¶

Try solving this:¶

hide_me

import ipywidgets as widgets
import IPython

answer = widgets.FloatText(value = 0, description='Your Answer')
op1 = widgets.Dropdown(value='', options={'Addition', 'Multiplication', 'Division', 'Brackets',''}, 
                         style={'description_width': 'initial'}, description='First Operation:',)
op2 = widgets.Dropdown(value='', options={'Addition', 'Multiplication', 'Division',''}, 
                         style={'description_width': 'initial'}, description='Second Operation:',)
op3 = widgets.Dropdown(value='', options={'Addition', 'Division',''}, 
                         style={'description_width': 'initial'}, description='Third Operation:',)
def display():
    print("Solve 7 * (9 - 4)/2 + 3 using the order of operations and write your answer below:")
    IPython.display.display(answer)
    
def check2(b):
    if op1.value =='':
        pass
    if op1.value == 'Brackets':
        print("Great! What did you do next?")
        IPython.display.display(op2)
    else:
        print("Remember the B in BEDMAS is for brackets, try the question again.")
        
def check3(c):
    if op2.value == '':
        pass
    if op2.value == 'Multiplication':
        print("Awesome! What did you do next?")
        IPython.display.display(op3)
    else:
        print("Remember division and multiplication are done left to right when there's no brackets and before addition and subtraction.\nTry the question again.")
        
def check4(d):
    if op3.value == '':
        pass
    if op3.value == 'Division':
        print("Well done! If you did not get 20.5, it must have been a calculation error, try each step again.")
    else:
        print("Remember division and multiplication are done before addition and subtraction, try the question again.")
        
def check(a):
    op1.value = ''
    op2.value = ''
    op3.value = ''
    IPython.display.clear_output(wait=False)
    display()
    if answer.value == 20.5:
        print("You are correct!")
    else:
        print("Sorry, that's not the right answer. Which operation did you do first?")
        IPython.display.display(op1)

display()
answer.observe(check, 'value')
op1.observe(check2, 'value')
op2.observe(check3, 'value')
op3.observe(check4, 'value')

Solve 7 * (9 - 4)/2 + 3 using the order of operations and write your answer below:

A few more questions¶

hide_me

import ipywidgets as widgets
import IPython

hide_me

choice = widgets.Dropdown(
    options={'Easy', 'Medium', 'Hard'},
    description='Difficulty:',
)
Start = widgets.Button(description = "Start")
ans = widgets.Button(description = "Answer")

def reveal(choice):
    click = False
    if choice=='Easy':
        print("2*5+3")
        print("10+3")
        print("13")
    else:
        if choice=='Medium':
            print("(1+6)*5+3")
            print("(7)*5+3")
            print("35+3")
            print("38")
        else:
            print("(4^2-2)/2*3^2")
            print("(16-2)/2*3^2")
            print("(14)/2*3^2")
            print("(14)/2*9")
            print("7*9")
            print("63") 

def create(choice):
    #click = True
    if choice=='Easy':
        print("2*5+3")
    else:
        if choice=='Medium':
            print("(1+6)*5+3")
        else:
            print("(4^2-2)/2*3^2")
            
def on_button(a):
    IPython.display.clear_output(wait=False)
    IPython.display.display(choice, Start, ans)
    reveal(choice.value)
    
            
def display2(b):
    IPython.display.clear_output(wait=False)
    IPython.display.display(choice, Start)
    create(choice.value)
    IPython.display.display(ans)
    ans.on_click(on_button)
    
    
IPython.display.display(choice, Start)
Start.on_click(display2)

Back to our first Problem¶

Now that you have some examples under your belt, let’s go back to the hard expression we saw earlier: