
import uiButtons
%uiButtons
Note: Please run the cell above, then click on “Initialize” to use this notebook.
Fractions and Addition¶
Introduction¶
A fraction is a number, but not necessarily a whole number.
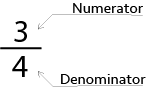
A fraction is written in the form \(\dfrac{a}{b}\), where \(a\) and \(b\) are integers, with \(b\neq 0\).
The number \(a\) (on top) is called the numerator and the number \(b\) (on the bottom) is called the denominator.
Fractions are used to represent parts of a whole “object”.
The denominator \(b\) tells us the number of equal parts an object is divided into.
The numerator \(a\) tells us how many of those parts we have.
For example, if a pizza is divided into 8 equal slices, and I eat 3 of them, then I’ve eaten \(\dfrac{3}{8}\) of a pizza.
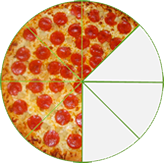
There are many cases where it is useful to add or subtract two fractions.
Let’s take Kevin as an example. He had two large pizzas at his birthday party: one pepperoni and one deluxe.
Each pizza was cut into 8 slices. If there are 3 slices of pepperoni pizza and 6 slices of deluxe pizza left over, how much pizza is left over in total?
What if the deluxe pizza was cut into 12 slices instead of 8?
These are examples where we must add two fractions to solve the problem.
This notebook will explore how to add and subtract fractions of two forms:
Two fractions with the same denominators (like fractions)
Two fractions with different denominators (unlike fractions)
Fractions (Quick Recap)¶
A fraction is a number that represents part of something.
 For example, the fraction \(\frac{1}{2}\) represents half of the integer 1. In other words, \(0.5\).
For example, the fraction \(\frac{1}{2}\) represents half of the integer 1. In other words, \(0.5\).
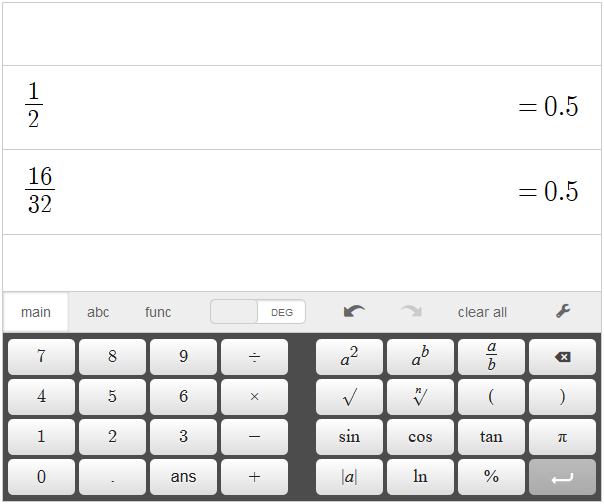
Statements like \(\frac{1}{2} = \frac{16}{32}\) can sometimes confuse people because it is not always easy to see how \(1\) might relate to \(16\) or how \(2\) might relate to \(32\), but in reality they both simply mean one half.
Another way to say \(\frac{1}{2}\) is to say \(1\) divided by \(2\).
As a little exercise, try inputting \(1\div 2\) into a calculator, then try \(16 \div 32\).
Did you get the same answer both times?
Let’s try another one, input \(1 \div 4\), then try \(77 \div 308\).
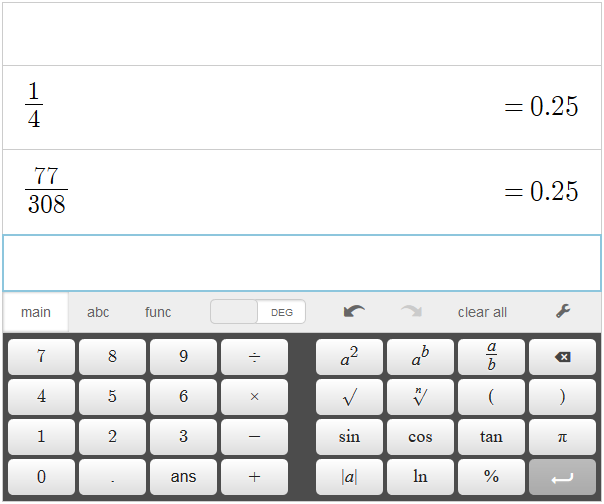
What is really happening is that the bottom number (the denominator) tells you how many equal parts the object is divided into, and the top number (the numerator) tells you how many of these equal parts we actually have. So for example if we cut a large pizza into \(2\) slices and take \(1\), or if we cut the same large pizza into \(32\) slices and take \(16\), we took the same amount of pizza in both cases, \(\dfrac{1}{2}\) (a half of the pizza)
There are three main categories when talking about fractions: proper, improper, and mixed.
A proper fraction is one where the numerator is less than the denominator, and it represents a number between 0 and 1.
An improper fraction is one where the numerator is larger than or equal to the denominator, and it represents a number greater than or equal to 1.
A mixed number is the sort of thing you might encounter in carpentry or a baking recipe, like \(3\,\frac14\) inches (it’s like saying \(3+\frac14\)), or \(1\,\frac12\) cups of flour (\(1+\frac12\)).
Mixed numbers and improper fractions are two different ways of expressing the same number, and it is possible to convert between them.
Fractions with the Same Denominators¶
The simplest fraction addition or subtraction happens when both denominators are the same. Let’s watch the video below before we do an example.
%%html
<div align="middle">
<iframe id="vid1" width="640" height="360" src="https://www.youtube.com/embed/qDc_-GTipBk" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen style="box-shadow: 3px 3px 12px #ACACAC"></iframe>
<p><a href="https://www.youtube.com/channel/UCBuMwlP7kHkNxdPAqtFSJTw" target="_blank">Click here</a> for more videos by Math Antics.</p>
</div>
<script>
var reachable = false;
$(function() {
var myFrame = $('#vid1');
var videoSrc = myFrame.attr("src");
myFrame.attr("src", videoSrc)
.on('load', function(){reachable = true;});
setTimeout(function() {
if(!reachable) {
var ifrm = myFrame[0];
ifrm = (ifrm.contentWindow) ? ifrm.contentWindow : (ifrm.contentDocument.document) ? ifrm.contentDocument.document : ifrm.contentDocument;
ifrm.document.open();
ifrm.document.write('If the video does not start click <a href="' + videoSrc + '" target="_blank">here</a>');
ifrm.document.close();
}
}, 2000)
});
</script>
Click here for more videos by Math Antics.
Now that we have a better understanding of how to add fractions with like denominators, let’s look at our pizza example from earlier. Kevin had two large pizzas at his birthday party: one pepperoni and one deluxe.
Each pizza was cut into 8 slices. If there are 3 slices of pepperoni pizza and 6 slices of deluxe pizza left over, how much pizza is left over in total?
Since each whole pizza was cut into \(8\) slices, they both have \(8\) as their denominators.
Therefore, \(3\) out of \(8\) slices of pepperoni are left and \(6\) out of \(8\) slices of deluxe are left.
To find out what fraction of pizza remains, we add: \(\frac{3}{8} + \frac{6}{8}\).
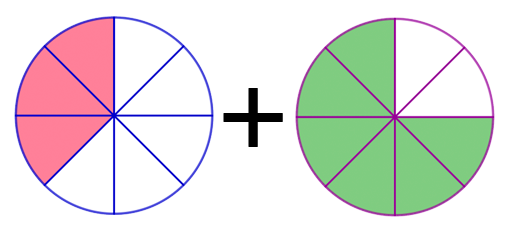
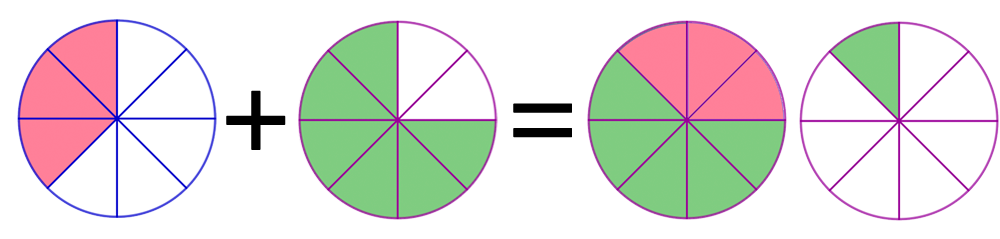
Now, since both fractions have the same denominator, all we need to do is add the numerators together:
Notice that the denominator stayed the same.
For this technique to work, we only add together the numerators and keep the common denominator.
Now, since \(\frac{8}{8}\) makes up an entire pizza and 9 is bigger than 8, we can subtract \(8\) from the numerator to get \(\frac{9}{8}=1\frac{1}{8}\) (turning an improper fraction into a mixed number \(1+\frac{1}{8}\)).
Looking at this result of \(1\frac{1}{8}\) (or \(1+\frac{1}{8}\)), we now know that there is an entire pizza plus one slice left over from the party.
Subtraction follows the same rules as addition.
Let’s assume we want to know how many slices of pepperoni pizza were eaten at the party.
We know the pizza was initially cut into 8 slices and only 3 remain, therefore
This means that \(5\) slices of pepperoni pizza were eaten.
Fractions with Different Denominators¶
Now we know how to add and subtract fractions with the same denominator (“like” fractions).
Next, let’s learn how to add fractions with different denominators (“unlike” fractions).
Going back to our pizza example, let’s assume the pepperoni pizza was cut into \(8\) slices but the deluxe pizza was cut into \(12\) slices instead.
Let’s say the pepperoni pizza has \(3\) slices left over, just like last time.
The fraction of that pizza that remains is \(\frac{3}{8}\).
Let’s say there are \(6\) slices of deluxe pizza left over.
That’s the same number as last time, but we had more slices to begin with.
The fraction of deluxe that remains is \(\frac{6}{12}\).
To find out how much is left, we add: \(\frac{3}{8}+\frac{6}{12}\).
Now, the first thing to keep in mind is that we must have common denominators before we can add the fractions together.
A popular method for getting a common denominator is to multiply each fraction by each other’s denominator.
Let’s watch the video below to help understand this concept.
%%html
<div align="middle">
<iframe id="vid2" width="640" height="360" src="https://www.youtube.com/embed/N-Y0Kvcnw8g?start=0&end=278" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen style="box-shadow: 3px 3px 12px #ACACAC"></iframe>
<p><a href="https://www.youtube.com/channel/UCBuMwlP7kHkNxdPAqtFSJTw" target="_blank">Click here</a> for more videos by Math Antics.</p>
</div>
<script>
$(function() {
var reachable = false;
var myFrame = $('#vid2');
var videoSrc = myFrame.attr("src");
myFrame.attr("src", videoSrc)
.on('load', function(){reachable = true;});
setTimeout(function() {
if(!reachable) {
var ifrm = myFrame[0];
ifrm = (ifrm.contentWindow) ? ifrm.contentWindow : (ifrm.contentDocument.document) ? ifrm.contentDocument.document : ifrm.contentDocument;
ifrm.document.open();
ifrm.document.write('If the video does not start click <a href="' + videoSrc + '" target="_blank">here</a>');
ifrm.document.close();
}
}, 2000)
});
</script>
Click here for more videos by Math Antics.
Now that we understand how to add unlike fractions, let’s solve our pizza problem from earlier.
Remember we had two pizzas: a pepperoni cut into \(8\) slices and a deluxe cut into \(12\) slices.
With this we came up with the following sum:
Using the method we learned from the video, let’s start by getting the common denominator.
Our fractions have \(8\) and \(12\) as denominators, so we will multiply each fraction by each other’s denominator:
So the answer is \(\frac{84}{96}\)!
This result may seem a little odd as we are talking about pizza slices:
It says we have \(84\) out of \(96\) slices left over.
This answer is correct, but it can be reduced.
Looking at \(84\) and \(96\), we can see they are both multiples of \(12\).
If we divide each number by \(12\), we can reduce our fraction.
Since \(84\div 12 = 7\) and \(96\div 12 = 8\), we can say \(\frac{84}{96}=\frac{7}{8}\).
This means there is \(\frac{7}{8}\) of a pizza left over.
Practice and Experiment¶
Now that we understand the difference between like and unlike fractions as well as how to add and subtract them, let’s do some practice.
Below is an interactive widget to help you visualize what happens when adding two fractions together.
You should see two pairs of boxes that look like fractions.
You can enter the fractions from our examples above or your own, then click start when ready.
%%html
<script src="./d3/d3.min.js"></script>
<script src="https://d3js.org/d3.v3.min.js"></script>
<script src="https://code.jquery.com/jquery-1.10.2.js"></script>
<style>
.divisionBox {
outline: solid #000000 3px;
fill: #ffffff;
opacity: 1.0;
z-index: -1;
}
.filledNum {
z-index: 99;
}
.fractionInput {
max-width: 50px;
}
.fractionText {
font: 25px serif;
fill: black;
}
.lOpperandDivisonBoxFractionText {
fill: red;
}
.rOpperandDivisonBoxFractionText {
fill: red;
}
.fractionBar {
max-width: 50px;
height: 3px;
background-color: #000000;
}
.buttons {
min-width: 40px;
width: 40px;
margin: 5px;
}
.mainButtons{
clear: left;
}
h1, p {
font-family: Helvetica, Arial, Sans-Serif;
}
input {
text-align: center;
}
</style>
%%html
<div>
<div>
<div style="float:left">
<input type="text" class="fractionInput form-control form-control-sm" id="lOppNumerator" placeholder="0" style="margin-bottom: -10px">
<hr align="left" class="fractionBar">
<input type="text" class="fractionInput form-control form-control-sm" id="lOppDenominator" placeholder="1" style="margin-top: -10px">
</div>
<div style="float: left; margin: 12px 20px 0 20px">
<h1>+</h1>
</div>
<div style="float: left; margin-left: 0px">
<input type="text" class="fractionInput form-control form-control-sm" id="rOppNumerator" placeholder="0" style="margin-bottom: -10px">
<hr align="left" class="fractionBar">
<input type="text" class="fractionInput form-control form-control-sm" id="rOppDenominator" placeholder="1" style="margin-top: -10px">
</div>
</div>
</div>
<div style="margin-left: 180px">
<h3>Enter two fractions to add together</h3>
</div>
<div style="clear:left; margin-top: 60px">
<button type="button" id="submitFraction" class="btn btn-primary buttons" style="float: left; min-width:100px">Start</button>
</div>
+
Enter two fractions to add together
%%html
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="-200 0 800 200">
<image class="speechBubbles resetDisplay" id="speech1" xlink:href="./images/Speech1.png" height="75" width="225" x="75" style="display: block"/>
<image class="speechBubbles resetDisplay" id="speech2" xlink:href="./images/Speech2.png" height="75" width="225" x="75" style="display: none"/>
<image class="speechBubbles resetDisplay" id="speech3" xlink:href="./images/Speech3.png" height="75" width="225" x="100" style="display: none"/>
<image class="speechBubbles resetDisplay" id="speech4" xlink:href="./images/Speech4.png" height="75" width="225" x="-150" style="display: none"/>
<image class="speechBubbles resetDisplay" id="speech5" xlink:href="./images/Speech5.png" height="75" width="225" x="75" style="display: none"/>
<image class="speechBubbles resetDisplay" id="speech6" xlink:href="./images/Speech6.png" height="75" width="225" x="75" style="display: none"/>
<image class="speechBubbles resetDisplay" id="speech7" xlink:href="./images/Speech7.png" height="75" width="225" x="75" style="display: none"/>
<image id="meow" xlink:href="./images/meow.png" height="190" width="60" x="-20" style="display: none"/>
<image id="pixelCat" xlink:href="./images/pixelCat.png" height="250" width="200" onmouseover="showMeow()" onmouseout="hideMeow()"/>
</svg>
<svg id="mainCanvas" style="float: left" viewBox="0 0 850 420">
<rect height="100" width="400" x="20" y="20" class="divisionBox"></rect>
<rect height="0" width="0" x="20" y="300" class="divisionBox" id="answerBox"></rect>
<rect height="100" width="400" x="20" y="20" class="divisionBox" id="lOpperandDivisonBox"></rect>
<rect height="100" width="0" x="20" y="20" class="filledNum" id="lOpperandDivisonBoxFilled"></rect>
<rect height="100" width="0" x="20" y="20" class="filledNum" id="lOpperandDivisonBoxAnswer"></rect>
<text x="0" y="148" color="black" font-size="30">+</text>
<rect height="100" width="400" x="20" y="160" class="divisionBox" id="rOpperandDivisonBox"></rect>
<rect height="100" width="0" x="20" y="160" class="filledNum" id="rOpperandDivisonBoxFilled"></rect>
<rect height="100" width="0" x="20" y="160" class="filledNum" id="rOpperandDivisonBoxAnswer"></rect>
<line x1="15" x2="425" y1="280" y2="280" stroke="black" stroke-width="3px"></line>
<image x="660" y="0" height="175px" width="175px" style="opacity:0" id="arrow" xlink:href="./images/speechbubble.png"/>
<foreignObject x="440" y="100" width="150" height="50" class="expandBtn resetDisplay" id="lOppExpandBtn"
style="display: none">
<body>
<lable style="float: left; margin-top:10px;">Multiply</lable>
<div class="btns" style="float: left; margin: 5px 0 0 5px;">
<button type="button" id="lOppExpandPlusBtn" class="btn btn-outline-primary btn-sm" style="width: 30px"><b>+</b></button>
<button type="button" id="lOppExpandMinusBtn" class="btn btn-outline-primary btn-sm" style="width: 30px"><b>-</b></button>
</div>
</body>
</foreignObject>
<foreignObject x="440" y="240" width="150" height="50" class="expandBtn resetDisplay" id="rOppExpandBtn"
style="display: none">
<body>
<lable style="float: left; margin-top:10px;">Multiply</lable>
<div class="btns" style="float: left; margin: 5px 0 0 5px;">
<button type="button" id="rOppExpandPlusBtn" class="btn btn-outline-primary btn-sm" style="width: 30px"><b>+</b></button>
<button type="button" id="rOppExpandMinusBtn" class="btn btn-outline-primary btn-sm" style="width: 30px"><b>-</b></button>
</div>
</body>
</foreignObject>
</svg>
</div>
<div style="clear: left; margin-left: 0px;">
<button type="button" id="addBtn" class="btn btn-primary buttons resetDisplay" style="display: none; float: left; min-width:100px">Combine</button>
</div>
<div class="mainButtons">
<button type="button" id="resetBtn" class="btn btn-primary buttons resetDisplay" style="display: none; clear: left; min-width:100px">Reset</button>
</div>
%%html
<div class="answerArea" id="answerAreaId" style="display: none;">
<svg width="130" height="100" id="answerCanvas" style="float: left; padding-right: 10px"></svg>
<div>
<input type="text" class="fractionInput form-control form-control-sm" id="answerNumerator" placeholder="0" style="margin-bottom: -10px">
<hr align="left" class="fractionBar">
<input type="text" class="fractionInput form-control form-control-sm" id="answerDenominator" placeholder="1" style="margin-top: -10px">
</div>
</div>
%%html
<div class="answerArea" style="display: none;">
<button id="checkAnswer" class="btn btn-primary">Check Answer</button>
</div>
<div>
<h5 id="correct" class="answerStatusText resetDisplay" style="display: none">Correct!</h5>
<h5 id="needRounding" class="answerStatusText resetDisplay" style="display: none">Correct but can be reduced.</h5>
<h5 id="incorrect" class="answerStatusText resetDisplay" style="display: none">Not quite, try again.</br>Don't forget to keep the original common denominator (only the numerators get added)</h5>
</div>
Correct!
Correct but can be reduced.
Not quite, try again.Don't forget to keep the original common denominator (only the numerators get added)
%%html
<script src="main.js">
</script>
Conclusion¶
Let’s review what we have learned today:
Proper fractions represent a number between \(0\) and \(1\).
Improper fractions represent a number greater than or equal to \(1\).
Unlike fractions require the same denominator before adding or subtracting.
Multiplying the top and bottom part of the fractions until we get a common denominator.
When adding or subtracting fractions, only the numerators are added or subtracted. The denominator remains the same.
So it turns out fractions are not so scary after all! They simply represent a number between \(0\) and \(1\) or a number greater than \(1\). With a little practice adding and subtracting fractions, you will become a fraction guru in no time!

