Counting triangles¶

In this notebook we explore two methods for counting the total number of triangles in a pentagon.
Organization of the notebook:

Section 1 discusses some preliminaries for the problem.
Section 2 presents an animation of counting triangles in a pentagon.
Section 3 presents an alternate method for counting triangles in a pentagon.
Section 4 concludes the notebook with some exercises.

1. Preliminaries¶

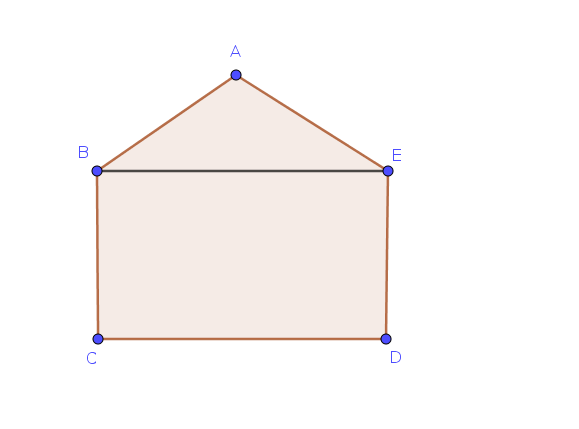
Let’s consider a pentagon \(ABCDE.\) If we connect \(B\) and \(E\) then we can divide the pentagon into a triangle, \(ABE\), and a rectangle, \(BCDE\).
So, our preliminary discussion will be to count how many triangles we get as we divide the triangle and rectangle.

1.1. Triangles in a triangle¶

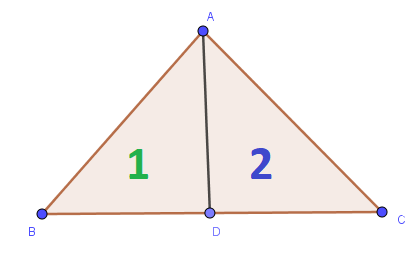
Let’s consider a triangle \(ABC\). First, we draw a line \(AD\) from \(A\) to \(BC\) as shown in the following figure.
We can see that there are two triangles: \(ABD\) and \(ACD.\)
Actually in this picture there are three different triangles, since we still count the original triangle \(ABC.\)

Now let’s add two points, \(D\) and \(E\), along the bottom, draw lines to them from \(A\), and see what we get.

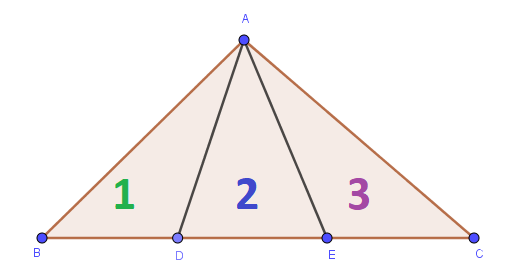
Let us find the all triangles for this scenario.

Step 1: consider all smaller triangles.
From the figure we can see that the large triangle \(ABC\) consists of three small triangles: \(ABD, ADE, ACE\).
Step 2: try to merge two small triangles to make a larger triangle.
For example, if we merge triangle \(ABD\) with \(ADE\) then we find \(ABE\). Similarly, we find \(ACD\).
Step 3: join three small triangles to generate larger one.
Merging all three small triangles we find triangle \(ABC.\)

In total, there are \(3+2+1=6\) triangles.

Now if we add one more line \(AF\) from \(A\) to line \(BC\), how many triangles do we get?.
Draw the triangle \(ABC\) and count the triangles.

There are now 4 small triangles.
There are three pairs of adjacent triangles we can combine to make larger triangles.
There are two ways to combine three triangles: the first three, or the last three.
As always, there is the original big triangle.

Did you find the answer? We have \(4+3+2+1=10\) triangles.

Can you guess how many triangles we’ll get if we add one more line from the top to the bottom?

With 0 lines, there was \(1\) triangle.
With 1 line, there were \(1+2=3\) triangles.
With 2 lines, there were \(1+2+3=6\) triangles.
With 3 lines, there were \(1+2+3+4=10\) triangles.

Did you guess 15 triangles for the next step? If so, well done!
The numbers that count how many triangles we have at each step are called the triangular numbers.

The name comes from something a child might observe while stacking blocks:
It’s the number of blocks you need to create a stack of blocks in the shape of a triangle:

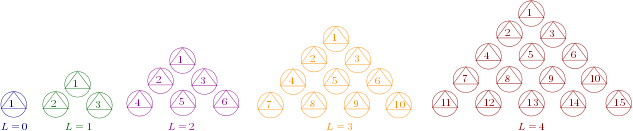In the above figure, L denotes the number of “lines” in a triangle.

If you’re comfortable with formulas, here’s a cool fact:
The number of blocks needed to make a triangular stack with \(n\) levels is \(\dfrac{n(n+1)}{2}\) ; where \(n = L + 1\)

There’s a fun (but maybe not entirely true) story associated with this formula:
As a child, the mathematician Carl Friederic Gauss was annoying his teacher one day.
To keep Gauss busy, the teacher asked him to add up the numbers from 1 to 100.
In a matter of minutes, Gauss discovered the formula, determined the answer (which is \(\dfrac{100\times 101}{2}=5050\)), and went back to annoying his teacher.

For better understanding consider the following animation. Change the slider value of \(n\) and observe how we count the triangles.

#ggb.material('tyvxr9ym').draw()

%%html
<iframe scrolling="no" title="TriangleAnimation" src="https://www.geogebra.org/material/iframe/id/cwbxjw9c/width/716/height/272/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="716px" height="272px" style="border:0px;"> </iframe>

1.2. Triangles in a rectangle¶

To determine the number of triangles in a rectangle, at first label every small triangle. The total number of triangles will be the double of highest labelling number. For example, consider a rectangle ABCD, where every vertex is connected with each other. If we start to label the smaller triangles from \(1\) we end up with four triangles. So, the total number of triangles is \(4 \times 2 = 8\). Now, play with the following animation.

#ggb.material('wzchjrrr').draw()

%%html
<iframe scrolling="no" title="QuadAnimation" src="https://www.geogebra.org/material/iframe/id/fn8pg8ut/width/697/height/322/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="697px" height="322px" style="border:0px;"> </iframe>

2. Triangles in a pentagon¶

Now that we’ve seen how to count how many triangles we get when we draw lines in a larger triangle, and how to count triangles in a rectangle, we put the two together, and determine the number of triangles in a pentagon, as the next animation demonstrates.

#ggb.material('exxjnzdn').draw()

%%html
<iframe scrolling="no" title="PentaAnimation" src="https://www.geogebra.org/material/iframe/id/b5xutv8n/width/723/height/314/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="723px" height="314px" style="border:0px;"> </iframe>

3. Alternate Method for counting triangles¶

There is a second method to count the triangles in a pentagon, when all vertices are connected.
This is the angular, or symmetry method. It relies on the following fact:

Rotating a regular pentagon by \(72^\circ\) (one fifth of a full rotation) produces the same pentagon.
(In other words, all that changes is the labelling of the corners.)

Here, we will count all similar triangles at a time.
There are seven distinct groups of triangles in a pentagon when all vertices are connected with each other.
The symmetry noted above tells us there are 5 triangles in each group.
So the total number of the triangles in the Pentagon is 7x5=35.

Let’s play the following animation to find the seven groups. The sliders \(n\) and \(i\) represent the number of groups and the number of triangles corresponding to a group, respectively.

#ggb.material('utabc8jy').draw()

%%html
<iframe scrolling="no" title="PentaMethod2" src="https://www.geogebra.org/material/iframe/id/eyudxdcw/width/765/height/341/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="765px" height="341px" style="border:0px;"> </iframe>

4. Test yourself¶

def display(question, answerList):
    print(question)
    IPython.display.display(answerList)

Consider the following triangle ABC:

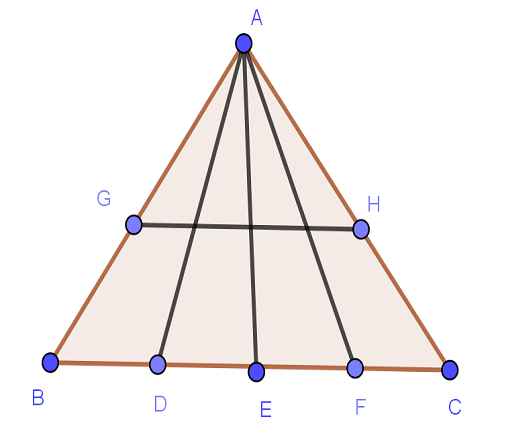
answer642 = widgets.RadioButtons(options=['Select the best one', '20', '10', '22', '12', 'None of the above'],
                             value = 'Select the best one',  description='Choices:')

question642 = "4.1 How many triangles are in the above triangle?"

def check642(g):
    IPython.display.clear_output(wait=False)
    display(question642, answer642)
    if answer642.value == '20':
        print("Correct Answer!")
    else:
        if answer642.value == 'Select the best one':
            pass
        else:
            print("Wrong answer! Try again.")

IPython.display.clear_output(wait=False)
display(question642, answer642)
answer642.observe(check642, 'value')

4.1 How many triangles are in the above triangle?

In the following figure two small rectangles (ADEF and BCEF) join each other and produce another large rectangle ABCD:

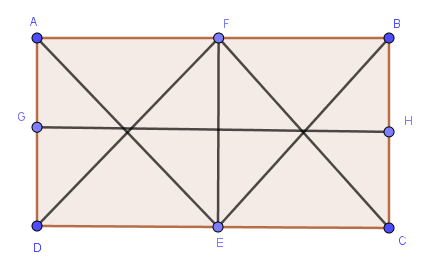
answer642 = widgets.RadioButtons(options=['Select the best one', '20', '22', '24', '26', 'None of the above'],
                             value = 'Select the best one',  description='Choices:')

question642 = "4.2 How many triangles are in the large rectangle?"

def check642(g):
    IPython.display.clear_output(wait=False)
    display(question642, answer642)
    if answer642.value == '26':
        print("Correct Answer!")
    else:
        if answer642.value == 'Select the best one':
            pass
        else:
            print("Wrong answer! Try again.")

IPython.display.clear_output(wait=False)
display(question642, answer642)
answer642.observe(check642, 'value')

4.2 How many triangles are in the large rectangle?

Consider a pentagon as drawn in the following figure:

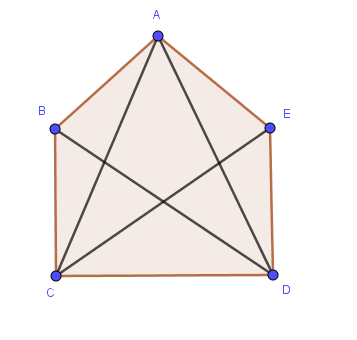
answer642 = widgets.RadioButtons(options=['Select the best one', '20', '17', '15', '13', 'None of the above'],
                             value = 'Select the best one',  description='Choices:')

question642 = "4.3 How many triangles are in the above pentagon?"

def check642(g):
    IPython.display.clear_output(wait=False)
    display(question642, answer642)
    if answer642.value == '17':
        print("Correct Answer!")
    else:
        if answer642.value == 'Select the best one':
            pass
        else:
            print("Wrong answer! Try again.")

IPython.display.clear_output(wait=False)
display(question642, answer642)
answer642.observe(check642, 'value')

4.3 How many triangles are in the above pentagon?

A pentagon ABCDE and a rectangle touch as like as the following figure:

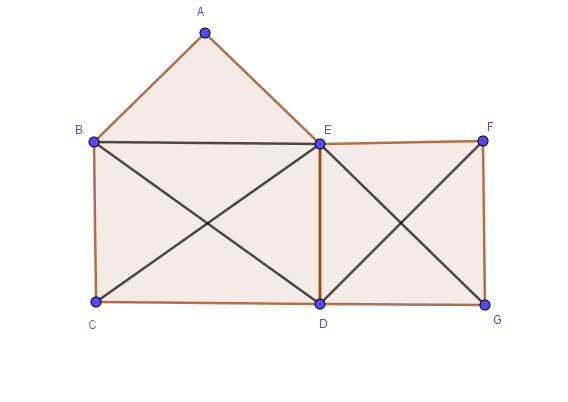
answer642 = widgets.RadioButtons(options=['Select the best one', '20', '18', '16', '14', 'None of the above'],
                             value = 'Select the best one',  description='Choices:')

question642 = "4.4 How many triangles are in the above figure?"

def check642(g):
    IPython.display.clear_output(wait=False)
    display(question642, answer642)
    if answer642.value == '18':
        print("Correct Answer!")
    else:
        if answer642.value == 'Select the best one':
            pass
        else:
            print("Wrong answer! Try again.")

IPython.display.clear_output(wait=False)
display(question642, answer642)
answer642.observe(check642, 'value')

4.4 How many triangles are in the above figure?

Again consider a pentagon:

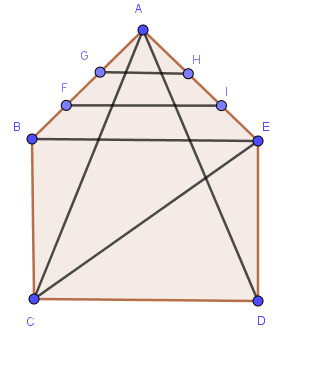
answer642 = widgets.RadioButtons(options=['Select the best one', '20', '24', '28', '29', 'None of the above'],
                             value = 'Select the best one',  description='Choices:')

question642 = "4.5 How many triangles are in the above pentagon?"

def check642(g):
    IPython.display.clear_output(wait=False)
    display(question642, answer642)
    if answer642.value == '28':
        print("Correct Answer!")
    else:
        if answer642.value == 'Select the best one':
            pass
        else:
            print("Wrong answer! Try again.")

IPython.display.clear_output(wait=False)
display(question642, answer642)
answer642.observe(check642, 'value')

4.5 How many triangles are in the above pentagon?

Callysto Curriculum Notebooks